题目内容
1.某中学一名数学老师对全班50名学生某次考试成绩分男女生进行了统计(满分150分),其中120分(含120分)以上为优秀,绘制了如下的两个频率分布直方图: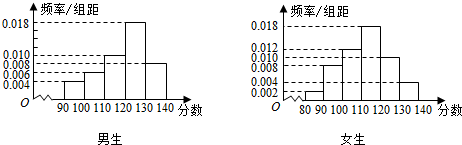
(1)根据如图两个直方图完成2×2列联表:
| 成绩性别 | 优秀 | 不优秀 | 总计 |
| 男生 | |||
| 女生 | |||
| 总计 |
| K0 | 2.072 | 2.076 | 3.814 | 5.024 | 6.635 | 7.879 | 10.828 |
| P(K2≥k0) | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
分析 (1)根据直方图,易得到列联表的各项数据.
(2)我们可以根据列联表中的数据,代入公式,计算出k值,然后代入离散系数表,比较即可得到答案.
解答 解:(1)
| 成绩性别 | 优秀 | 不优秀 | 总计 |
| 男生 | 13 | 10 | 23 |
| 女生 | 7 | 20 | 27 |
| 总计 | 20 | 30 | 50 |
∵K2≈4.844≥3.841,∴有95%的把握认为学生的数学成绩与性别之间有关系.
点评 本小题主要考查独立性检验的基本思想、方法及其简单应用等知识,考查或然与必然的数学思想方法,以及数据处理能力、运算求解能力和应用意识.

练习册系列答案
 新编小学单元自测题系列答案
新编小学单元自测题系列答案 字词句段篇系列答案
字词句段篇系列答案
相关题目
13.由某个2×2列联表数据计算得随机变量K2的观测值k=6.879,则下列说法正确的是( )
| P(K2≥k0) | 0.40 | 0.25 | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| k0 | 0.708 | 1.323 | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
| A. | 两个分类变量之间有很强的相关关系 | |
| B. | 有99%的把握认为两个分类变量没有关系 | |
| C. | 在犯错误的概率不超过1.0%的前提下认为这两个变量间有关系 | |
| D. | 在犯错误的概率不超过0.5%的前提下认为这两个变量间有关系 |
11.曲线y=sinx+ex(其中e=2.71828…是自然对数的底数)在点(0,1)处的切线的斜率为( )
| A. | 2 | B. | 3 | C. | $\frac{1}{3}$ | D. | $\frac{1}{2}$ |