题目内容

12．观察下列等式：13=12，13+23=（1+2）2，13+23+33=（1+2+3）2，13+23+33+43=（1+2+3+4）2，…，根据上述规律，第n个等式为：13+23+33+…+n3=（1+2+3+…+n）2=$\frac{{n}^{2}•（n+1）^{2}}{4}$．

分析 左边是连续自然数的立方和，右边是左边的数的和的立方，由此得到结论

解答 解：∵13=1
13+23=9=（1+2）2，
13+23+33=36=（1+2+3）2，
13+23+33+43=100=（1+2+3+4）2，
…
由以上可以看出左边是连续自然数的立方和，右边是左边的数的和的立方，
照此规律，第n个等式可为：13+23+33+…+n3=（1+2+3+…+n）2=$\frac{{n}^{2}•（n+1）^{2}}{4}$．
故答案为：13+23+33+…+n3=（1+2+3+…+n）2=$\frac{{n}^{2}•（n+1）^{2}}{4}$

点评 本题考查了归纳推理，归纳推理的一般步骤是：（1）通过观察个别情况发现某些相同性质，（2）从已知某些相同性质中推出一个明确表达的一般性命题

练习册系列答案
相关题目
2．已知a，b均为实数，logb（3a-1）为正数，点（b，a）在圆（x-$\frac{1}{2}$）2+（y+$\frac{1}{3}$）2=c2上，其中c＞0，则c的取值范围是（$\frac{2}{3}$，$\frac{\sqrt{5}}{2}$）∪（$\frac{\sqrt{5}}{2}$，+∞）．
3．设复数z满足z（2-3i）=6+4i（其中i为虚数单位），则z的模为2．
20．已知z1=2-3i，z2=$\frac{3+2i}{（2+i）^{2}}$，则$\frac{{z}_{1}}{{z}_{2}}$=4-3i．
7．已知二次函数y=x2-2ax+1在区间（2，3）上是单调函数，则实数a的取值范围是（　　）
A．a≤-3或a≥-2B．2≤a≤3C．a≤2或a≥3D．-3≤a≤-2
17．设函数$y={x^{\frac{1}{2}}}$，则导函数y′=$\frac{1}{2}{x^{-\frac{1}{2}}}$．
4．已知{an}是等差数列，其中a1=13，a4=7
（1）求{an}的通项；
（2）数列{an}前多少项和最大？最大和为多少？
（3）求|a1|+|a3|+|a5|+|a7|+|a9|+|a11|值．
1．某中学一名数学老师对全班50名学生某次考试成绩分男女生进行了统计（满分150分），其中120分（含120分）以上为优秀，绘制了如下的两个频率分布直方图：

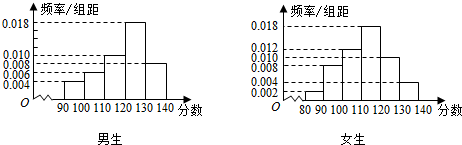
（1）根据如图两个直方图完成2×2列联表：
成绩性别优秀不优秀总计
男生
女生
总计
（2）根据（1）中表格的数据计算，你有多大把握认为学生的数学成绩与性别之间有关系？
K02.0722.0763.8145.0246.6357.87910.828
P（K2≥k0）0.150.100.050.0250.0100.0050.001
2．设α是锐角，sinα=$\frac{4}{5}$．求：
（1）cosα的值；
（2）sin（α+$\frac{π}{3}$）的值．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网