题目内容
9.已知数列{an}的前n项和为Sn,且a1=$\frac{1}{2},{a_{n+1}}=\frac{n+1}{2n}{a_n}$.(1)求{an}的通项公式;
(2)设bn=n(2-Sn),n∈N*,若bn≤λ,n∈N*恒成立,求实数λ的取值范围.
(3)设Cn=$\frac{{({2-{S_n}})}}{n(n+1)},n∈{N^*}$,Tn是数列{Cn}的前n项和,证明$\frac{3}{4}$≤Tn<1.
分析 (1)先化简递推公式,由等比数列的定义判断出:数列$\{\frac{a_n}{n}\}$是公比为$\frac{1}{2}$的等比数列,根据等比数列的通项公式求出an;
(2)由(1)和条件求出bn,利用作差法判断出数列{bn}的单调性,可求出bn的最大值,再求实数λ的取值范围;
(3)由(1)化简Cn=$\frac{(2-{S}_{n})}{n(n+1)}$,利用裂项相消法求出Tn,利用函数的单调性判断出Tn的单调性,结合n的取值范围求出Tn的范围,即可证明结论.
解答 解:(1)由已知得$\frac{{{a_{n+1}}}}{n+1}=\frac{1}{2}\frac{a_n}{n}$,其中n∈N*
∴数列$\{\frac{a_n}{n}\}$是公比为$\frac{1}{2}$的等比数列,
又首项${a_1}=\frac{1}{2}$,则$\frac{a_n}{n}={(\frac{1}{2})^n}$,∴${a_n}=n{(\frac{1}{2})^n}$….4分
(2)由(1)知${S_n}=\frac{1}{2}+\frac{2}{2^2}+\frac{3}{2^3}+…+\frac{n}{2^n}$
∴$\frac{1}{2}{S_n}=\frac{1}{2^2}+\frac{2}{2^3}+\frac{3}{2^4}…+\frac{n}{{{2^{n+1}}}}$
两式相减得:$\frac{1}{2}{S_n}=\frac{1}{2}+\frac{1}{2^2}+\frac{1}{2^3}+…+\frac{1}{2^n}-\frac{n}{{{2^{n+1}}}}$,
∴$\frac{1}{2}{S_n}=1-\frac{n+2}{{{2^{n+1}}}}$,∴${S_n}=2-\frac{n+2}{2^n}$….7分
∵bn=n(2-Sn),∴${b_n}=\frac{n(n+2)}{2^n}$,
∴${b_{n+1}}-{b_n}=\frac{(n+1)(n+3)}{{{2^{n+1}}}}-\frac{n(n+2)}{2^n}=\frac{{-{n^2}+3}}{{{2^{n+1}}}}$
则当n=1,b2-b1>0,即b2>b1,
当n≥2,bn+1-bn<0,即bn+1<bn,b2是最大项且b2=2,
∴λ≥2.….9分
证明:(3)由(1)得,${C}_{n}=\frac{(2-{S}_{n})}{n(n+1)}=\frac{n+2}{{2}^{n}•n(n+1)}=\frac{1}{{2}^{n}}(\frac{n+2}{n}-\frac{n+2}{n+1})=2(\frac{1}{n{2}^{n}}-\frac{1}{(n+1){2}^{n+1}})$,
∴${T_n}=2(\frac{1}{{{2^1}•1}}-\frac{1}{{{2^2}•2}}+\frac{1}{{{2^2}•2}}-\frac{1}{{{2^3}•3}}+…+\frac{1}{{n•{2^n}}}-\frac{1}{{(n+1)•{2^{n+1}}}})$=$1-\frac{1}{{{2^n}(n+1)}}$…12分
又令f(n)=$\frac{1}{{{2^n}(n+1)}}$,显然f(n)在n∈N*时单调递减,
∴0<f(n)≤f(1)=$\frac{1}{4}$,
故$\frac{3}{4}≤{T_n}<1$…13分.
点评 本题考查等比数列的定义、通项公式,裂项相消法求数列的和,以及数列的函数特征和判断数列单调性的方法:作差法、基本初等函数的单调性,考查化简、变形能力,属于中档题.

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案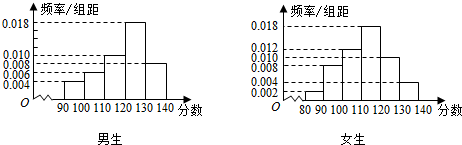
(1)根据如图两个直方图完成2×2列联表:
| 成绩性别 | 优秀 | 不优秀 | 总计 |
| 男生 | |||
| 女生 | |||
| 总计 |
| K0 | 2.072 | 2.076 | 3.814 | 5.024 | 6.635 | 7.879 | 10.828 |
| P(K2≥k0) | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
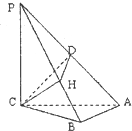 三棱锥P-ABC,PC⊥面ABC,△PAC是等腰三角形,PA=4,AB⊥BC,CH⊥PB,垂足为H,D是PA的中点,则△CDH的面积最大时,CB的长是( )
三棱锥P-ABC,PC⊥面ABC,△PAC是等腰三角形,PA=4,AB⊥BC,CH⊥PB,垂足为H,D是PA的中点,则△CDH的面积最大时,CB的长是( )| A. | $\frac{\sqrt{5}}{3}$ | B. | $\frac{2\sqrt{5}}{3}$ | C. | $\frac{\sqrt{6}}{3}$ | D. | $\frac{2\sqrt{6}}{3}$ |