在等比数列{an}中.已知a2=2.a5=16．(1)求数列{an}的通项公式,(2)若数列{bn}是首项为1.公差为1的等差数列.求数列{an+bn}的前n项和Tn．题目和参考答案——青夏教育精英家教网——

题目内容

6．在等比数列{a_n}中，已知a₂=2，a₅=16．
（1）求数列{a_n}的通项公式；
（2）若数列{b_n}是首项为1，公差为1的等差数列，求数列{a_n+b_n}的前n项和T_n．

分析（1）由等比数列的通项公式求出求出a₁和公比q，代入通项公式求出a_n；
（2）由等差数列的通项公式求出b_n，再代入a_n+b_n化简，利用等差、等比数列的前n项和公式和分组求和法，求出数列{a_n+b_n}的前n项和T_n．

解答解：（1）设等比数列{a_n}的公比是q，
∵a₂=2，a₅=16，∴ ${q}^{3}=\frac{{a}_{5}}{{a}_{2}}$ =8，则q=2，
∴a₁= $\frac{{a}_{2}}{q}$ =1，则a_n=2^n-1；
（2）∵数列{b_n}是首项为1，公差为1的等差数列，
∴b_n=1+（n-1）×1=n，则a_n+b_n=2^n-1+n，
∴数列{a_n+b_n}的前n项和T_n=（1+2+2²+…+2^n-1）+（1+2+3+…+n）
= $\frac{1{-2}^{n}}{1-2}$ $+\frac{n（1+n）}{2}$ = ${2}^{n}+\frac{（n-1）（n+2）}{2}$ ．

点评本题考查等差、等比数列的通项公式，以及前n项和公式，以及分组求和法的应用，属于中档题．

练习册系列答案

课课练与单元测试系列答案

世纪金榜小博士单元期末一卷通系列答案

单元测试AB卷台海出版社系列答案

黄冈新思维培优考王单元加期末卷系列答案

名校名师夺冠金卷系列答案

小学英语课时练系列答案

培优新帮手系列答案

天天向上一本好卷系列答案

小学生10分钟应用题系列答案

课堂作业广西教育出版社系列答案

相关题目

16．（1）已知m＞n＞0，p＞0，证明：

\frac{n}{m} ＜ \frac{n + p}{m + p}

$\frac{n}{m}＜\frac{n+p}{m+p}$ ；
（2）△ABC中，证明：

\frac{s i n C}{s i n A + s i n B} + \frac{s i n A}{s i n B + s i n C} + \frac{s i n B}{s i n C + s i n A} ＜ 2

$\frac{sinC}{sinA+sinB}+\frac{sinA}{sinB+sinC}+\frac{sinB}{sinC+sinA}＜2$ ．

y = x^{\frac{1}{2}}

$y={x^{\frac{1}{2}}}$ ，则导函数y′=

\frac{1}{2} x^{- \frac{1}{2}}

$\frac{1}{2}{x^{-\frac{1}{2}}}$ ．

14．已知向量

\to a ， \to b

$\overrightarrow a，\overrightarrow b$ 满足：

| \to a | = | \to a + \to b | = 1

$|{\overrightarrow a}|=|{\overrightarrow a+\overrightarrow b}|=1$ ，

| \to b | = 2

$|{\overrightarrow b}|=2$ ，则向量

\to a

$\overrightarrow a$ 与

\to b

$\overrightarrow b$ 的夹角为180°．

1．某中学一名数学老师对全班50名学生某次考试成绩分男女生进行了统计（满分150分），其中120分（含120分）以上为优秀，绘制了如下的两个频率分布直方图：

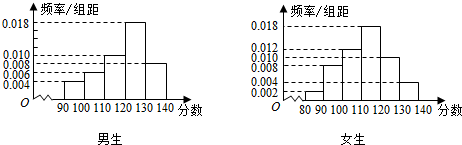
（1）根据如图两个直方图完成2×2列联表：

成绩性别	优秀	不优秀	总计
男生
女生
总计

（2）根据（1）中表格的数据计算，你有多大把握认为学生的数学成绩与性别之间有关系？

K₀	2.072	2.076	3.814	5.024	6.635	7.879	10.828
P（K²≥k₀）	0.15	0.10	0.05	0.025	0.010	0.005	0.001

\frac{x^{2}}{2}

$\frac{x^2}{2}$ +y²=1的离心率是（　　）

\frac{1}{4}

$\frac{1}{4}$

\frac{\sqrt{2}}{2}

$\frac{{\sqrt{2}}}{2}$

\frac{1}{2}

$\frac{1}{2}$

\frac{\sqrt{3}}{2}

$\frac{{\sqrt{3}}}{2}$

18．已知函数f（x）是偶函数，且x≥0时，f（x）=x²-2x+3，试求f（x）在R上的表达式，并画出图象，根据图象写出它的单调区间．

15．①已知抛物线y²=2x上的点与A（0，6）距离最近的点的坐标为（2，2）；
②已知不等式3ax-2lnx≥0对任意x＞0恒成立，则实数a的取值范围是[

\frac{2}{3 e}

$\frac{2}{3e}$ ，+∞）．

如图所示，A（m，

\sqrt{3}

$\sqrt{3}$ m）和B（n，-

\sqrt{3}

$\sqrt{3}$ n）两点分别在射线OS，OT（点S，T分别在第一，四象限）上移动，且

- - \to O A

$\overrightarrow{OA}$ •

- - \to O B

$\overrightarrow{OB}$ =-

\frac{1}{2}

$\frac{1}{2}$ ，O为坐标原点，动点P满足

- - \to O P

$\overrightarrow{OP}$ =

- - \to O A

$\overrightarrow{OA}$ +

- - \to O B

$\overrightarrow{OB}$ ．
（Ⅰ）求mn的值；
（Ⅱ）求动点P的轨迹方程，并说明它表示什么曲线．