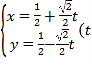题目内容
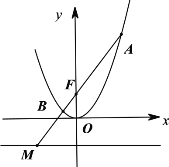
【题目】已知抛物线C:y2=4x与椭圆E:![]() 1(a>b>0)有一个公共焦点F.设抛物线C与椭圆E在第一象限的交点为M.满足|MF|
1(a>b>0)有一个公共焦点F.设抛物线C与椭圆E在第一象限的交点为M.满足|MF|![]() .
.
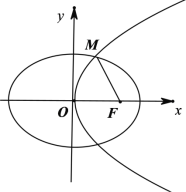
(1)求椭圆E的标准方程;
(2)过点P(1,![]() )的直线交抛物线C于A、B两点,直线PO交椭圆E于另一点Q.若P为AB的中点,求△QAB的面积.
)的直线交抛物线C于A、B两点,直线PO交椭圆E于另一点Q.若P为AB的中点,求△QAB的面积.
【答案】(1)![]() ;(2)
;(2)![]() .
.
【解析】
(1)由抛物线的定义可得![]() ,则M(
,则M(![]() ,
,![]() ),再由椭圆的定义可得
),再由椭圆的定义可得![]() ,即可求得
,即可求得![]() ,进而求解;
,进而求解;
(2)设A(x1,y1),B(x2,y2),利用斜率公式可得![]() ,即可得到直线AB的方程,再由点到直线距离可得点
,即可得到直线AB的方程,再由点到直线距离可得点![]() 到直线
到直线![]() 的距离
的距离![]() ,联立抛物线和直线
,联立抛物线和直线![]() ,进而利用弦长公式求得
,进而利用弦长公式求得![]() ,则
,则![]() ,即可求解.
,即可求解.
(1)由抛物线方程可得F(1,0),则椭圆的另一个焦点![]() ,
,
因为![]() ,∴M(
,∴M(![]() ,
,![]() ),
),
则2a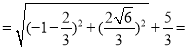 4,则a=2,
4,则a=2,
所以![]() ,
,
所以椭圆E的标准方程为![]() .
.
(2)设A(x1,y1),B(x2,y2),点P(1,![]() )在椭圆上,则Q(﹣1,
)在椭圆上,则Q(﹣1,![]() ),
),
因为P为AB的中点,且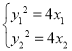 ,
,
则kAB![]() ,
,
故直线AB的方程为y![]() (x﹣1),即8x﹣6y+1=0,
(x﹣1),即8x﹣6y+1=0,
∴Q到直线AB的距离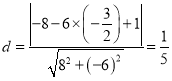 ,
,
联立![]() ,整理得64x2﹣128x+1=0,
,整理得64x2﹣128x+1=0,
故x1+x2=2,x1x2![]() ,
,
则![]() ,
,
所以![]()
![]() .
.

练习册系列答案
相关题目