题目内容
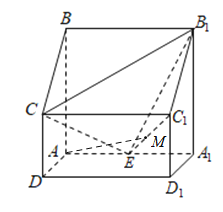
【题目】如图,正三棱柱![]() 中,(底面为正三角形,侧棱垂直于底面),侧棱长
中,(底面为正三角形,侧棱垂直于底面),侧棱长![]() ,底面边长
,底面边长![]() ,
,![]() 是
是![]() 的中点.
的中点.
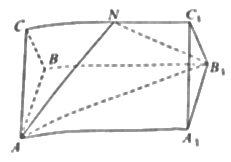
(1)求证:平面![]() 平面
平面![]() ;
;
(2)设![]() 是线段
是线段![]() 的中点,求直线
的中点,求直线![]() 与平面
与平面![]() 所成的角的正弦值.
所成的角的正弦值.
【答案】(1) 见解析(2)![]()
【解析】
(1)通过做平行线构造平行四边形,进而得到线面垂直,再由平形四边行的对边平行的性质得到平面![]() 内的线垂直于平面
内的线垂直于平面![]() 内的线,进而得到面面垂直;(2)建立空间坐标系,求直线
内的线,进而得到面面垂直;(2)建立空间坐标系,求直线![]() 的方向向量和面
的方向向量和面![]() 的法向量,进而得到线面角.
的法向量,进而得到线面角.
(1)证明:取![]() 中点
中点![]() ,
,![]() 的中点为M,连结
的中点为M,连结![]() ,MN,则有
,MN,则有![]() ∥
∥![]() 且
且![]() =
=![]() ∴四边形
∴四边形![]() 为平行四边形,
为平行四边形,![]() ∥
∥![]()
∵![]() 面
面![]() ,
,![]()
∴![]() ,又
,又![]()
∴![]() 平面
平面![]() 故
故![]() ⊥平面
⊥平面![]() .
.
所以平面![]() 平面
平面![]()
(2)如图建立空间直角坐标系,则B(-![]() ,0,0),A(
,0,0),A(![]() ,0,0),
,0,0),![]()
![]()
因为![]() 是线段
是线段![]() 的中点,所以M
的中点,所以M![]()
所以![]()

设![]() 是平面
是平面![]() 的一个法向量,因为
的一个法向量,因为![]()
![]()
所以,由
所以可取![]()


练习册系列答案
相关题目