题目内容
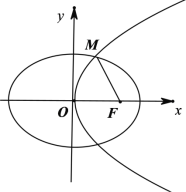
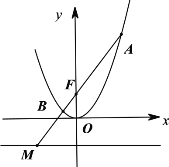
【题目】已知抛物线C:x2=2py(p>0)的焦点为F.过F的直线与抛物线C交于A、B,与抛物线C的准线交于M.
(1)若|AF|=|FM|=4,求常数p的值;
(2)设抛物线C在点A、B处的切线相交于N,求动点N的轨迹方程.
【答案】(1)2;(2)y![]() .
.
【解析】
(1)设交点F(0,![]() ),则准线方程为y
),则准线方程为y![]() ,根据F为AM的中点可得
,根据F为AM的中点可得![]() y1
y1![]() 2p,即可求得
2p,即可求得![]() ;
;
(2)由![]() 可得
可得![]() ,即可求得切线斜率,联立抛物线与直线AB,根据韦达定理可得x1+x2=2pk,x1x2=﹣p2,利用点斜式直线方程可得在点
,即可求得切线斜率,联立抛物线与直线AB,根据韦达定理可得x1+x2=2pk,x1x2=﹣p2,利用点斜式直线方程可得在点![]() 的切线方程,联立即可求得点
的切线方程,联立即可求得点![]() ,即可得到点
,即可得到点![]() 的轨迹方程.
的轨迹方程.
(1)由抛物线的方程可得焦点坐标F(0,![]() ),准线方程为y
),准线方程为y![]() ,
,
设A(x1,y1),B(x2,y2),
因为|AF|=|FM|=4,所以F为AM的中点,所以y1![]() 2p,
2p,
所以2p=4,解得p=2
(2)由y![]() ,所以
,所以![]() ,设直线AB:y=kx
,设直线AB:y=kx![]() ,
,
与抛物线C的方程联立得:x2﹣2pkx﹣p2=0,则![]() =4p2k2+4p2>0,
=4p2k2+4p2>0,
所以x1+x2=2pk,x1x2=﹣p2,
则在点A处的切线方程为:y﹣y1![]() (x﹣x1),即py+py1=x1x,
(x﹣x1),即py+py1=x1x,
同理可得B处的切线方程py+py2=x2x,
联立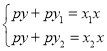 ,解得xN
,解得xN![]() pk,yN
pk,yN![]() ,
,
所以N的轨迹方程为y![]() ,
,

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目