题目内容
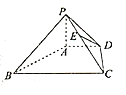
【题目】如图，直三棱柱ABC-A1B1C1中，D,E分别是AB，BB1的中点.
（Ⅰ）证明： BC1//平面A1CD;
（Ⅱ）设AA1= AC=CB=2，AB=2
，求三棱锥C一A1DE的体积.
【答案】（Ⅰ）见解析（Ⅱ）
【解析】
试题（Ⅰ）连接AC1交A1C于点F，则DF为三角形ABC1的中位线，故DF∥BC1．再根据直线和平面平行的判定定理证得BC1∥平面A1CD．（Ⅱ）由题意可得此直三棱柱的底面ABC为等腰直角三角形，由D为AB的中点可得CD⊥平面ABB1A1．求得CD的值，利用勾股定理求得A1D、DE和A1E的值，可得A1D⊥DE．进而求得S△A1DE的值，再根据三棱锥C-A1DE的体积为
S△A1DECD，运算求得结果
试题解析：（1）证明：连结AC1交A1C于点F，则F为AC1中点又D是AB中点，
连结DF，则BC1∥DF． 3分
因为DF平面A1CD，BC1不包含于平面A1CD， 4分
所以BC1∥平面A1CD． 5分
（2）解：因为ABC﹣A1B1C1是直三棱柱，所以AA1⊥CD．由已知AC=CB，D为AB的中点，所以CD⊥AB．又AA1∩AB=A，于是CD⊥平面ABB1A1． 8分
由AA1=AC=CB=2，
得∠ACB=90°，
，
，
，A1E=3，故A1D2+DE2=A1E2，即DE⊥A1D 10分
所以三菱锥C﹣A1DE的体积为：
=
=1． 12分
练习册系列答案
相关题目
