题目内容
【题目】已知函数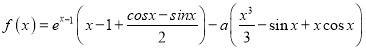 在
在![]() 内有两个极值点x1,x2(x1<x2),其中a为常数.
内有两个极值点x1,x2(x1<x2),其中a为常数.
(1)求实数a的取值范围;
(2)求证:x1+x2>2.
【答案】(1)a>1;(2)证明见解析.
【解析】
(1)转化问题为![]() 有两个变号零点,设
有两个变号零点,设![]() ,利用导函数可得
,利用导函数可得![]() 在
在![]() 上单调递增,则
上单调递增,则![]() ,即转化问题为
,即转化问题为![]() 有两个变号零点,即
有两个变号零点,即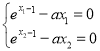 ,则
,则![]() ,设
,设![]() ,则直线y=a与
,则直线y=a与![]() 在x∈(0,+∞)有两个交点,进而利用导函数求
在x∈(0,+∞)有两个交点,进而利用导函数求![]() 的最值,即可求解;
的最值,即可求解;
(2)由(1),若x1+x2>2,则g(x2)>g(2﹣x1),即g(x1)>g(2﹣x1),构造函数F(x)=g(x)﹣g(2﹣x),进而证明x∈(0,1)时F(x)>0即可.
(1)因为![]() ,
,
由题意知x1,x2是导函数![]() 的变号零点,
的变号零点,
令![]() ,则
,则![]() ,所以
,所以![]() 在
在![]() 上单调递增,
上单调递增,
又![]() ,所以
,所以![]() ,
,
所以x1,x2是![]() 的两个零点,即
的两个零点,即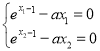 ,则
,则![]() ,
,
又令![]() ,则g(x1)=g(x2),
,则g(x1)=g(x2),
从而只需直线y=a与函数g(x)![]() 的图象在x∈(0,+∞)上有两个交点,
的图象在x∈(0,+∞)上有两个交点,
由![]() 可得当
可得当![]() 时,
时,![]() ;当
;当![]() 时,
时,![]() ,
,
所以g(x)在(0,1)递减,在(1,+∞)递增,
从而![]() ,
,
所以a>1.
(2)证明:由(1)知,0<x1<1<x2,
若不等式x1+x2>2成立,则g(x2)>g(2﹣x1),即g(x1)>g(2﹣x1),
令F(x)=g(x)﹣g(2﹣x),x∈(0,1),则只需F(x)>0,
而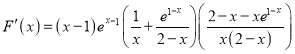 ,只需研究
,只需研究![]() 的符号,
的符号,
因为![]() ,
,![]() ,
,
所以![]() ,
,
所以![]() ,则
,则![]() ,
,
所以![]() ,
,
即x1+x2>2成立.

练习册系列答案
 快乐小博士巩固与提高系列答案
快乐小博士巩固与提高系列答案
相关题目