题目内容

19．若向量$\overrightarrow{a}$=（2，-x）与$\overrightarrow{b}$=（x，-8）的夹角为钝角，则x的范围为x＜0且x≠-4．

分析 由夹角为钝角得到数量积小于0，同时排除反向的情况．

解答 解：因为向量$\overrightarrow{a}$=（2，-x）与$\overrightarrow{b}$=（x，-8）的夹角为钝角，所以$\overrightarrow{a}•\overrightarrow{b}$=2x+8x＜0且x2≠16，
所以x＜0且x≠-4．
故答案为：x＜0且x≠-4．

点评 本题考查了向量的夹角与数量积的关系；注意向量夹角为钝角与数量积小于0不等价．

练习册系列答案
相关题目
9．对任意实数a，b定义运算“?”：a?b=$\left\{\begin{array}{l}{b，a-b≥1}\\{a，a-b＜1}\end{array}\right.$，设f（x）=（x2-1）?（4+x），若函数y=f（x）+k恰有三个零点，则实数k的取值范围是-2≤k＜1．
10．设公比q（q＞0）的等比数列{an}的前n项和Sn，若S2=3a2+2，S4=3a4+2，求公比q．
7．设公差不等于零的等差数列{an}的前n项和为Sn，且S5=30，a1，a2，a4成等比数列
（1）求数列{an}的通项公式；
（2）求$\frac{1}{{{a_1}{a_2}}}+\frac{1}{{{a_2}{a_3}}}+…+\frac{1}{{{a_{20}}{a_{21}}}}$的值．
14．若坐标原点到抛物线x2=$\frac{1}{m}$y的准线距离为2，则m=（　　）
A．$\frac{1}{8}$B．±$\frac{1}{8}$C．8D．±8
4．若f（x）=sin$\frac{π}{3}$-cosx，则f′（a）等于（　　）
A．sinαB．cosαC．sin$\frac{π}{3}$+cosαD．cos$\frac{π}{3}$+sinα
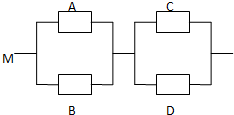11．如图，用A、B、C、D表示四类不同的元件连接成系统M．当元件A、B至少有一个正常工作且元件C、D至少有一个正常工作时，系统M正常工作．已知元件A、B、C、D正常工作的概率依次为：0.3、0.6、0.5、0.8，元件连接成的系统M正常工作的概率P（M）=0.648．
8．（$\frac{1-i}{1+i}$）2016=（　　）
A．1B．iC．-1D．-i
9．已知定义在R上的函数f（x）=ex+x2-x+sinx，则函数y=f（x）在点（0，f（0））处的切线方程为（　　）
A．y=3x-2B．y=x+1C．y=2x-1D．y=-2x+3

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网