题目内容
9.对任意实数a,b定义运算“?”:a?b=$\left\{\begin{array}{l}{b,a-b≥1}\\{a,a-b<1}\end{array}\right.$,设f(x)=(x2-1)?(4+x),若函数y=f(x)+k恰有三个零点,则实数k的取值范围是-2≤k<1.分析 化简函数f(x)的解析式,作出函数y=f(x)的图象,由题意可得,函数y=f(x)与y=-k的图象有3个交点,结合图象求得结果..
解答 解:当(x2-1)-(x+4)<1时,f(x)=x2-1,(-2<x<3),
当(x2-1)-(x+4)≥1时,f(x)=x+4,(x≥3或x≤-2),
函数y=f(x)=$\left\{\begin{array}{l}{{x}^{2}-1,(-2<x<3)}\\{x+4,(x≤-2,或x≥3)}\end{array}\right.$的图象如图所示: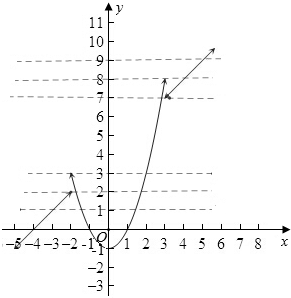
由图象得:要使函数y=f(x)+k恰有三个零点,只要函数f(x)与y=-k的图形由三个交点即可,
所以-1<-k≤2,所以-2≤k<1;
故答案为:-2≤k<1.
点评 本题主要考查数形结合解决函数的零点个数问题,关键是正确画图、识图;体现了化归与转化、数形结合的数学思想,属于中档题.

练习册系列答案
相关题目
8.已知集合A={y|y=x2+1,x∈R},B={y|y=5-x2,x∈R},则A∪B=( )
| A. | R | B. | [1,5] | C. | (-∞,-1]∪[5,+∞) | D. | {(-$\sqrt{2}$,3)($\sqrt{2}$,3)} |
1.“x=0”是“(2x-1)x=0”的( )
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充分必要条件 | D. | 既不充分也不必要条件 |
18.设函数f(x)=$\sqrt{3}$sinωx+cosωx,ω∈(-3,0),若f(x)的最小正周期为π,则f(x)的一个单调递减区间是( )
| A. | (-$\frac{π}{2}$,0) | B. | (-$\frac{π}{6}$,$\frac{π}{3}$) | C. | ($\frac{π}{3}$,$\frac{5π}{6}$) | D. | ($\frac{π}{2}$,π) |