题目内容
【题目】设复数![]() .
.
(1)若z在复平面内对应的点在第三象限,求m的取值范围;
(2)若z在复平面内对应的点在直线x-y-1=0上,求m的值.
【答案】(1){m|-1<m<0}。(2)m=1±![]() 。
。
【解析】
(1)根据复数的表示,列出不等式组,即可求解相应的实数![]() 的取值范围;
的取值范围;
(2)根据复数的表示,得到点(log2(1+m),log ![]() (3-m))在直线x-y-1=0上,代入列出方程,即可求解.
(3-m))在直线x-y-1=0上,代入列出方程,即可求解.
(1)由已知得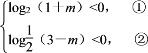
由①得-1<m<0,由②得m<2,
故不等式组的解集为{m|-1<m<0},
因此m的取值范围是{m|-1<m<0}.
(2)由已知得,点(log2(1+m),log ![]() (3-m))在直线x-y-1=0上,
(3-m))在直线x-y-1=0上,
即log2(1+m)-log ![]() (3-m)-1=0,
(3-m)-1=0,
整理得log2(1+m)(3-m)=1,
从而(1+m)(3-m)=2,
即m2-2m-1=0,
解得m=1±![]() ,
,
经验证得,当m=1±![]() 时,都能使1+m>0,且3-m>0,
时,都能使1+m>0,且3-m>0,
所以m=1±![]() .
.

练习册系列答案
 各地期末复习特训卷系列答案
各地期末复习特训卷系列答案 小博士期末闯关100分系列答案
小博士期末闯关100分系列答案 名校名师培优作业本加核心试卷系列答案
名校名师培优作业本加核心试卷系列答案
相关题目

