题目内容
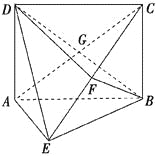
【题目】如图所示,矩形ABCD中,AD⊥平面ABE,AE=EB=BC=2,F为CE上的点,且BF⊥平面ACE.
(1)求证:AE⊥平面BCE;
(2)求证:AE∥平面BFD;
(3)求三棱锥C-BGF的体积.
【答案】(1)见详解;(2)见详解;(3)![]()
【解析】
(1)证明 ∵AD⊥平面ABE,AD∥BC, ∴BC⊥平面ABE,则AE⊥BC.
又∵BF⊥平面ACE,则AE⊥BF,
又BC∩BF=B,∴AE⊥平面BCE.
(2)证明 由题意可得G是AC的中点,连结FG,
∵BF⊥平面ACE,∴CE⊥BF.
而BC=BE,∴F是EC的中点,
在△AEC中,FG∥AE,∴AE∥平面BFD.
(3)∵AE∥FG.
而AE⊥平面BCE,
∴FG⊥平面BCF.
∵G是AC中点,F是CE中点,
∴FG∥AE且FG=![]() AE=1.
AE=1.
∴Rt△BCE中,BF=CE=CF=![]() ,
,
∴S△CFB=![]() ×
×![]() ×
×![]() =1.
=1.
∴VC-BGF=VG-BCF=·S△CFB·FG=![]() .
.

练习册系列答案
相关题目
【题目】为了解某班学生喜好体育运动是否与性别有关,对本班50人进行了问卷调查得到了如下的列联表:
喜好体育运动 | 不喜好体育运动 | |
男生 | 5 | |
女生 | 10 |
已知按喜好体育运动与否,采用分层抽样法抽取容量为10的样本,则抽到喜好体育运动的人数为6.
(1)请将上面的列联表补充完整;
(2)能否在犯错概率不超过0.01的前提下认为喜好体育运动与性别有关?说明你的理由;
(3)在上述喜好体育运动的6人中随机抽取两人,求恰好抽到一男一女的概率.
参考公式:![]() .
.
独立性检验临界值表:
| 0.10 | 0.05 | 0.025 | 0.010 |
| 2.706 | 3.841 | 5.024 | 6.635 |