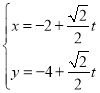Question

【题目】已知椭圆C：的右焦点为F，点A（一2，2)为椭圆C内一点。若椭圆C上存在一点P，使得｜PA｜＋｜PF｜＝8，则m的取值范围是（ ）．

A. B. ［9，25］ C. D. ［3，5］

Answer 1

【答案】A

【解析】

设椭圆的左焦点为F'（﹣2，0），由椭圆的定义可得2＝|PF|+|PF'|，即|PF'|＝2﹣|PF|，可得|PA|﹣|PF'|＝8﹣2，运用三点共线取得最值，解不等式可得m的范围，再由点在椭圆内部，可得所求范围．

椭圆C：的右焦点F（2，0），

左焦点为F'（﹣2，0），

由椭圆的定义可得2＝|PF|+|PF'|，

即|PF'|＝2﹣|PF|，

可得|PA|﹣|PF'|＝8﹣2，

由||PA|﹣|PF'||≤|AF'|＝2，

可得﹣2≤8﹣2≤2，

解得，所以,①

又A在椭圆内，

所以,所以8m-16<m(m-4),解得或,

与①取交集得

故选：A．