题目内容
【题目】在
的
个元素的子集中，称元素之和为偶数的子集为偶集合，元素之和为奇数的子集为奇集合.试求偶集合数目与奇集合数目之差
.
【答案】见解析
【解析】
先把集合
的
个元素的子集按是否包含
分成两组.
在不包含的组中，存在一个偶集合与奇集合之间的一一对应
.
因此，在该组中，偶集合数目与奇集合数目之差为0.
从而，
即为包含的组中偶集合数目与奇集合数目之差，这些集合是由和集合
中的
个元素组成的.
故
. ①
同样地，
.
注意到，在的
个元素的子集中偶集合数目与奇集合数目相等.
若
，则
为偶集合与奇集合之间的一一对应.
故
. ②
因而，
. ③
接下来考虑
.
仍把集合的个元素的子集按是否包含
分成两组.
结合式①、③得
. ④
设
.则式④为
由
，及
，再比较式⑤得
. ⑥
由式①、②、③，及结论⑥得
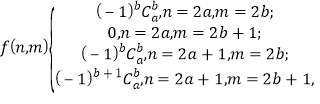
其中，
、
.
练习册系列答案
名校课堂系列答案
相关题目
