题目内容
已知函数f(x)=xm-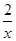 且f(4)=
且f(4)=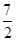 .
.
(1)求m的值;
(2)判定f(x)的奇偶性;
(3)判断f(x)在(0,+∞)上的单调性,并给予证明.
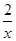 且f(4)=
且f(4)=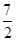 .
.(1)求m的值;
(2)判定f(x)的奇偶性;
(3)判断f(x)在(0,+∞)上的单调性,并给予证明.
(1)m=1
(2)奇函数
(3)见解析
(2)奇函数
(3)见解析
解:(1)∵f(4)=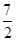 ,∴4m-
,∴4m- =
=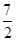 ,
,
∴m=1.
(2)由(1)知f(x)=x-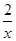 ,
,
∴函数的定义域为(-∞,0)∪(0,+∞),
关于原点对称.
又f(-x)=-x+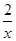 =-(x-
=-(x-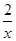 )=-f(x),
)=-f(x),
所以函数f(x)是奇函数.
(3)函数f(x)在(0,+∞)上是单调增函数,证明如下:设x1>x2>0,
则f(x1)-f(x2)=x1-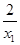 -(x2-
-(x2- )=(x1-x2)(1+
)=(x1-x2)(1+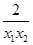 ),
),
因为x1>x2>0,
所以x1-x2>0,1+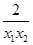 >0.
>0.
所以f(x1)>f(x2).
所以函数f(x)在(0,+∞)上为单调递增函数.
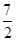 ,∴4m-
,∴4m- =
=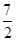 ,
,∴m=1.
(2)由(1)知f(x)=x-
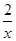 ,
,∴函数的定义域为(-∞,0)∪(0,+∞),
关于原点对称.
又f(-x)=-x+
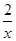 =-(x-
=-(x-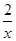 )=-f(x),
)=-f(x),所以函数f(x)是奇函数.
(3)函数f(x)在(0,+∞)上是单调增函数,证明如下:设x1>x2>0,
则f(x1)-f(x2)=x1-
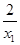 -(x2-
-(x2- )=(x1-x2)(1+
)=(x1-x2)(1+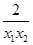 ),
),因为x1>x2>0,
所以x1-x2>0,1+
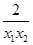 >0.
>0.所以f(x1)>f(x2).
所以函数f(x)在(0,+∞)上为单调递增函数.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
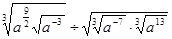 ;
;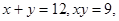 且
且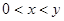 ,求
,求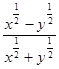 的值.
的值.
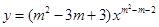 的图像不过坐标原点,则
的图像不过坐标原点,则 的值是___ .
的值是___ . 点
点 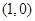 点
点 轴右侧
轴右侧  轴上方
轴上方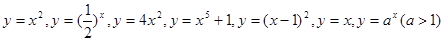 上述函数是幂函数的个数是( )
上述函数是幂函数的个数是( ) 个
个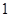 个
个
 个
个 个
个