题目内容
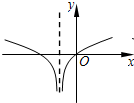
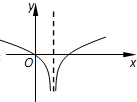
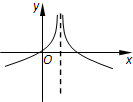
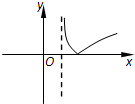
函数y=e|lnx|-|x-1|的图象大致是( )
A. | B. | C. | D. |
由y=e|lnx|-|x-1|可知:函数过点(1,1),
当0<x<1时,y=e-lnx-1+x=
+x-1,y′=-
+1<0.
∴y=e-lnx-1+x为减函数;若当x>1时,y=elnx-x+1=1,
故选D.
当0<x<1时,y=e-lnx-1+x=
| 1 |
| x |
| 1 |
| x2 |
∴y=e-lnx-1+x为减函数;若当x>1时,y=elnx-x+1=1,
故选D.

练习册系列答案
相关题目
 点
点 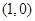 点
点 轴右侧
轴右侧  轴上方
轴上方