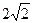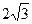题目内容
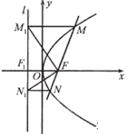
如图,过抛物线y2=2PX(P>0)的焦点F的直线与抛物线相交于M、N两点,自M、N向准线L作垂线,垂足分别为M1、N1
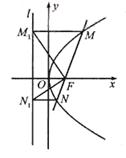
(Ⅰ)求证:FM1⊥FN1:
(Ⅱ)记△FMM1、、△FM1N1、△FN N1的面积分别为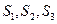 ,试判断S22=4S1S3是否成立,并证明你的结论。
,试判断S22=4S1S3是否成立,并证明你的结论。 


(Ⅰ)求证:FM1⊥FN1:
(Ⅱ)记△FMM1、、△FM1N1、△FN N1的面积分别为
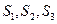 ,试判断S22=4S1S3是否成立,并证明你的结论。
,试判断S22=4S1S3是否成立,并证明你的结论。 

(Ⅰ) 略(Ⅱ)成立。
本小题主要考查抛物线的概念,抛物线的几何性质等平面解析几何的基础知识,考查综合运用数学知识进行推理运算的能力(满分13分)
(1) 证法1:由抛物线的定义得
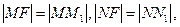


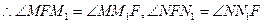 2分
2分
如图,设准线l与x的交点为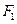
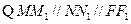
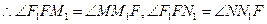
而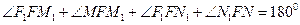
即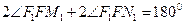
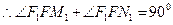
故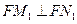
证法2:依题意,焦点为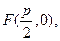 准线l的方程为
准线l的方程为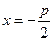
设点M,N的坐标分别为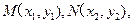 直线MN的方程为
直线MN的方程为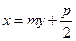 ,则有
,则有
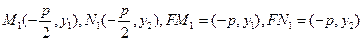
由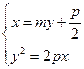 得
得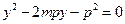
于是,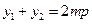 ,
,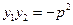
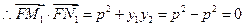 ,故
,故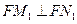
(Ⅱ)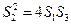 成立,证明如下:
成立,证明如下:
证法1:设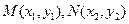 ,则由抛物线的定义得
,则由抛物线的定义得
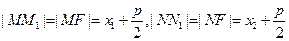 ,于是
,于是
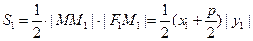
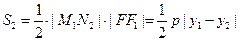
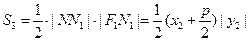
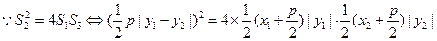
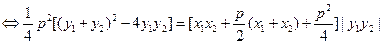
将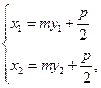 与
与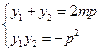 代入上式化简可得
代入上式化简可得 

 ,此式恒成立。
,此式恒成立。
故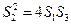 成立。
成立。
证法2:如图,设直线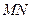 M的倾角为
M的倾角为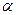 ,
,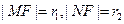
则由抛物线的定义得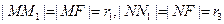
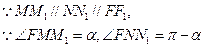
于是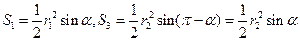
在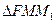 和
和 中,由余弦定理可得
中,由余弦定理可得
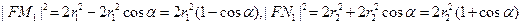
由(I)的结论,得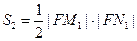
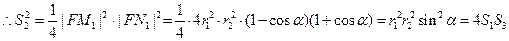
即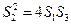 ,得证。
,得证。
(1) 证法1:由抛物线的定义得
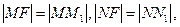


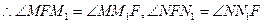 2分
2分如图,设准线l与x的交点为
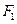

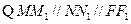
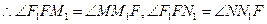
而
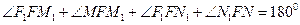
即
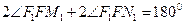
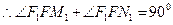
故
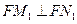
证法2:依题意,焦点为
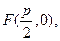 准线l的方程为
准线l的方程为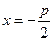
设点M,N的坐标分别为
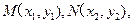 直线MN的方程为
直线MN的方程为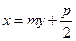 ,则有
,则有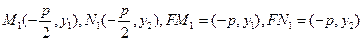
由
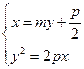 得
得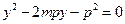
于是,
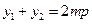 ,
,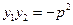
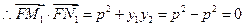 ,故
,故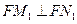
(Ⅱ)
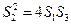 成立,证明如下:
成立,证明如下:证法1:设
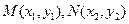 ,则由抛物线的定义得
,则由抛物线的定义得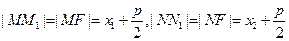 ,于是
,于是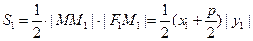
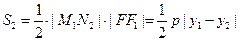
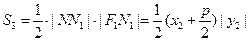
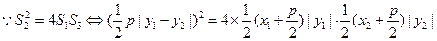
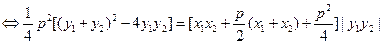
将
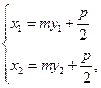 与
与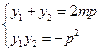 代入上式化简可得
代入上式化简可得 

 ,此式恒成立。
,此式恒成立。故
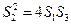 成立。
成立。证法2:如图,设直线
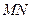 M的倾角为
M的倾角为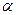 ,
,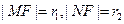
则由抛物线的定义得
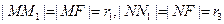
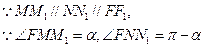
于是
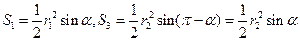
在
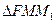 和
和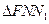 中,由余弦定理可得
中,由余弦定理可得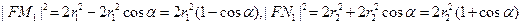
由(I)的结论,得
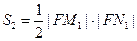
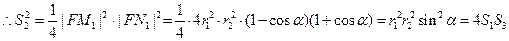
即
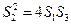 ,得证。
,得证。
练习册系列答案
相关题目


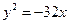 上一点到焦点的距离为
上一点到焦点的距离为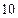 ,求该点的坐标。
,求该点的坐标。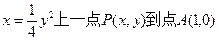 的距离为3,又点
的距离为3,又点 的面积为( )
的面积为( )