题目内容
经过抛物线y2=4x的焦点且平行于直线3x-2y=0的直线l的方程是______．
∵抛物线y2=4x的焦点坐标为（1，0），
∴过抛物线的焦点和直线3x-2y=0的直线方程可设为3x-2y+m=0，
则3+m=0，
解得m=-3．
∴对应的直线方程为3x-2y-3=0，
故答案为：3x-2y-3=0．
∴过抛物线的焦点和直线3x-2y=0的直线方程可设为3x-2y+m=0，
则3+m=0，
解得m=-3．
∴对应的直线方程为3x-2y-3=0，
故答案为：3x-2y-3=0．
练习册系列答案
一线名师权威作业本系列答案
相关题目
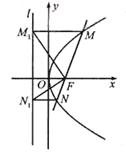
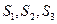，试判断S22＝4S1S3是否成立，并证明你的结论。 
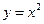上到直线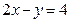
的距离最短的点的坐标是（ ）
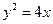上一点
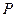到焦点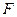
的距离是
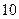，则
