题目内容
【题目】已知抛物线![]() 的焦点为
的焦点为![]() 为抛物线
为抛物线![]() 上位于第一象限内的点,过点
上位于第一象限内的点,过点![]() 的直线
的直线![]() 交抛物线
交抛物线![]() 于另一点
于另一点![]() ,交
,交![]() 轴的正半轴于点
轴的正半轴于点![]() .
.
(1)若点![]() 的横坐标为
的横坐标为![]() ,且
,且![]() 与双曲线
与双曲线![]() 的实轴长相等,求抛物线
的实轴长相等,求抛物线![]() 的方程;
的方程;
(2)对于(1)中求出的抛物线![]() ,若点
,若点![]() ,记点
,记点![]() 关于
关于![]() 轴的对称点为
轴的对称点为![]() (不同于点
(不同于点![]() ),直线
),直线![]() 交
交![]() 轴于点
轴于点![]() .
.
①求证:点![]() 的坐标为
的坐标为![]() ;
;
②若![]() ,求点
,求点![]() 到直线
到直线![]() 的距离
的距离![]() 的取值范围.
的取值范围.
【答案】(1) ![]() (2) ①见证明; ②
(2) ①见证明; ②![]()
【解析】
(1)由题意得![]() ,故
,故![]() ,于是可得抛物线方程.(2)①设直线
,于是可得抛物线方程.(2)①设直线![]() 的方程为
的方程为![]() ,代入抛物线方程后得到关于
,代入抛物线方程后得到关于![]() 的二次方程,然后结合根与系数的关系及
的二次方程,然后结合根与系数的关系及![]() 三点共线并由向量的共线可证得结论成立;②由
三点共线并由向量的共线可证得结论成立;②由![]() 可得
可得![]() 为等腰直角三角形,所以
为等腰直角三角形,所以![]() ,整理可得
,整理可得![]() ,两边平方后结合根与系数的关系得到
,两边平方后结合根与系数的关系得到![]() ,且
,且![]() .再由题意得到
.再由题意得到![]() ,令
,令![]() ,可得
,可得![]() ,最后构造函数可得所求范围.
,最后构造函数可得所求范围.
(1)由题意,知![]() ,
,
∵![]() 与双曲线
与双曲线![]() 的实轴长相等,
的实轴长相等,
∴![]() ,解得
,解得![]() ,
,
∴抛物线![]() 的方程为
的方程为![]() .
.
(2)①由题意,可设直线![]() 的方程为
的方程为![]() ,
,
由 消去
消去![]() 整理得
整理得![]() ,
,
∵![]() ,
,
∴![]() .
.
设![]() ,则
,则![]() ,
,
由题意得![]() ,
,
设![]() 点坐标为
点坐标为![]() ,则
,则![]() ,
,
由题意知![]() ,
,
∴![]() ,
,
即![]() .
.
又![]() ,
,
∴![]() ,
,
显然![]() ,
,
∴![]() ,
,
∴点![]() 的坐标为
的坐标为![]() .
.
②由题意,![]() 为等腰直角三角形,
为等腰直角三角形,
∴![]() ,即
,即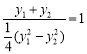 ,
,
∴![]() ,
,
∴![]() ,即
,即![]() ,
,
∴![]() ,且
,且![]() ,
,
又![]() ,所以
,所以![]() .
.
又点![]() 到直线
到直线![]() 的距离
的距离![]() .
.
令![]() ,则
,则![]() ,且
,且![]() ,
,
∴![]() .
.
设![]() ,则
,则![]() 在
在![]() 上为减函数,
上为减函数,
∴![]() ,即
,即![]() ,
,
∴![]() 的取值范围为
的取值范围为![]() .
.

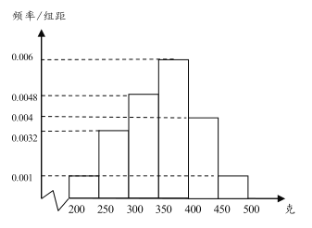
【题目】设某校新、老校区之间开车单程所需时间为![]() ,
,![]() 只与道路畅通状况有关,对其容量为
只与道路畅通状况有关,对其容量为![]() 的样本进行统计,结果如图:
的样本进行统计,结果如图:
| 25 | 30 | 35 | 40 |
频数(次) | 20 | 30 | 40 | 10 |
(1)求![]() 的分布列与数学期望
的分布列与数学期望![]() ;
;
(2)刘教授驾车从老校区出发,前往新校区做一个50分钟的讲座,结束后立即返回老校区,求刘教授从离开老校区到返回老校区共用时间不超过120分钟的概率.
【题目】某公司培训员工某项技能,培训有如下两种方式:
方式一:周一到周五每天培训1小时,周日测试
方式二:周六一天培训4小时,周日测试
公司有多个班组,每个班组60人,现任选两组![]() 记为甲组、乙组
记为甲组、乙组![]() 先培训;甲组选方式一,乙组选方式二,并记录每周培训后测试达标的人数如表:
先培训;甲组选方式一,乙组选方式二,并记录每周培训后测试达标的人数如表:
第一周 | 第二周 | 第三周 | 第四周 | |
甲组 | 20 | 25 | 10 | 5 |
乙组 | 8 | 16 | 20 | 16 |
![]() 用方式一与方式二进行培训,分别估计员工受训的平均时间
用方式一与方式二进行培训,分别估计员工受训的平均时间![]() 精确到
精确到![]() ,并据此判断哪种培训方式效率更高?
,并据此判断哪种培训方式效率更高?
![]() 在甲乙两组中,从第三周培训后达标的员工中采用分层抽样的方法抽取6人,再从这6人中随机抽取2人,求这2人中至少有1人来自甲组的概率.
在甲乙两组中,从第三周培训后达标的员工中采用分层抽样的方法抽取6人,再从这6人中随机抽取2人,求这2人中至少有1人来自甲组的概率.