题目内容
已知数列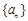 满足
满足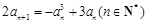 且
且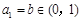
(1) 证明: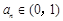 ;
;
(2) 比较an与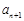 的大小;
的大小;
(3) 是否存在正实数c,使得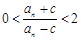 ,对一切
,对一切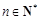 恒成立?若存在,则求出c的取值范围;若不存在,说明理由.
恒成立?若存在,则求出c的取值范围;若不存在,说明理由.
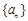 满足
满足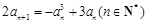 且
且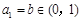
(1) 证明:
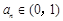 ;
;(2) 比较an与
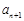 的大小;
的大小;(3) 是否存在正实数c,使得
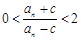 ,对一切
,对一切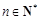 恒成立?若存在,则求出c的取值范围;若不存在,说明理由.
恒成立?若存在,则求出c的取值范围;若不存在,说明理由.(1)见解析
(2)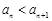
(3)存在正实数c,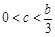 ,使
,使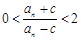 ,对
,对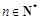 恒成立
恒成立
(2)
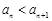
(3)存在正实数c,
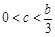 ,使
,使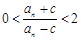 ,对
,对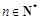 恒成立
恒成立 (1) 令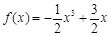 ,则当
,则当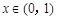 时
时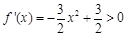 ,
,
∴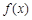 在(0,1)上为增函数,由
在(0,1)上为增函数,由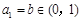 知,
知,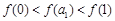 .
.
∴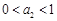 以下可用数学归纳法证明
以下可用数学归纳法证明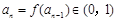 .
.
(2) ∵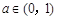
∴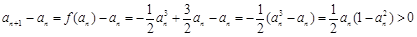
∴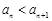
(3)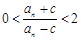
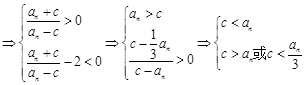
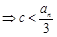 对
对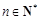 恒成立
恒成立
由(2)知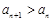 ,∴ {an}为递增数列,
,∴ {an}为递增数列,
∴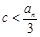 ,对
,对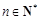 恒成立
恒成立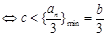 ,
,
∴存在正实数c,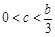 ,使
,使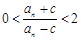 ,对
,对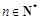 恒成立.
恒成立.
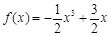 ,则当
,则当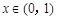 时
时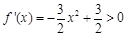 ,
,∴
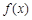 在(0,1)上为增函数,由
在(0,1)上为增函数,由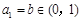 知,
知,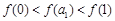 .
.∴
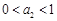 以下可用数学归纳法证明
以下可用数学归纳法证明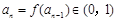 .
.(2) ∵
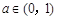
∴
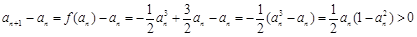
∴
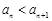
(3)
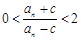
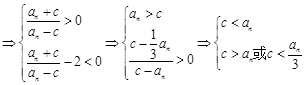
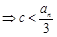 对
对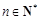 恒成立
恒成立由(2)知
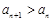 ,∴ {an}为递增数列,
,∴ {an}为递增数列,∴
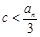 ,对
,对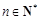 恒成立
恒成立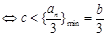 ,
,∴存在正实数c,
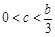 ,使
,使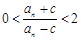 ,对
,对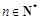 恒成立.
恒成立.
练习册系列答案
相关题目
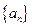 ,如果
,如果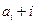 (
( =1,2,3,…)为完全平方数,则称数
=1,2,3,…)为完全平方数,则称数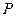 性质”。
性质”。 具有“
具有“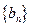 ,且
,且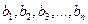 是
是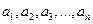 的一个排列
的一个排列 ;②数列
;②数列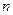 项和
项和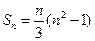 ,证明数列
,证明数列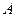 :1,2,3,…,
:1,2,3,…,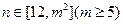 时,
时,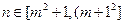 时,数
时,数 列
列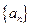 为等差数列,且
为等差数列,且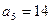 ,
, ,数列
,数列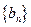 的前
的前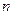 项和为
项和为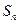 ,
,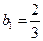 且
且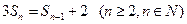 ;,
;,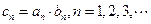 ,
,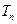 为数列
为数列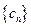 的前
的前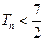 .
.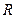 的二次函数
的二次函数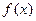 的最小值为
的最小值为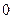 且
且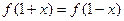 ,直线
,直线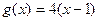 被
被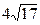 ,数列
,数列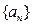 满足
满足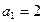 ,
,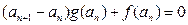
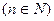 ,设
,设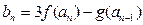 求
求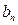 的最值及相应的
的最值及相应的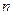
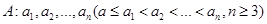 具有性质P:对任意
具有性质P:对任意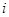 ,
,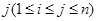 ,
,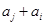 与
与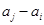 两数中至少有一个是该数列中的一项,现给出以下四个命题:
两数中至少有一个是该数列中的一项,现给出以下四个命题: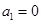 ;
;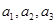
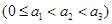 具有性质P,则
具有性质P,则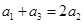
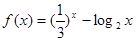 ,正实数
,正实数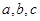 是公差为正数的等差数列,且满足
是公差为正数的等差数列,且满足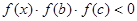 。若实数
。若实数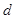 是方程
是方程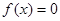 的一个解,那么下列四个判断:
的一个解,那么下列四个判断: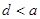 ;②
;②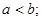 ③
③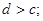 ④
④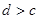 中有可能成立的个数为 ( )
中有可能成立的个数为 ( )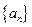 是等比数列,
是等比数列,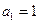 ,公比q是
,公比q是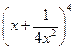 的展开式的第二项(按x的降幂排列)求数列
的展开式的第二项(按x的降幂排列)求数列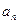 与前n项和
与前n项和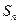 。
。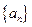 中,
中,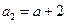 (
(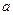 为常数),
为常数),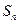 为
为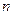 项和,且
项和,且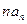 与
与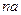 的等差中项.
的等差中项.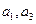 ;
;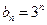 且
且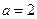 ,
,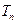 为数列
为数列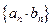 的前
的前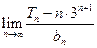 的值.
的值.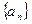 中,
中,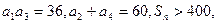 求
求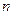 的范围.
的范围.