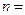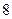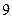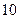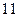题目内容
(本小题满分12分)
设数列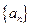 为等差数列,且
为等差数列,且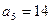 ,
, ,数列
,数列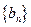 的前
的前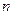 项和为
项和为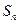 ,
,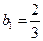 且
且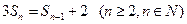 ;,
;,
(Ⅰ)求数列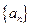 ,
,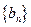 的通项公式;
的通项公式;
(Ⅱ)若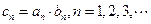 ,
,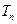 为数列
为数列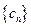 的前
的前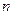 项和. 求证:
项和. 求证: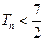 .
.
设数列
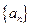 为等差数列,且
为等差数列,且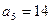 ,
, ,数列
,数列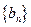 的前
的前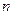 项和为
项和为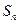 ,
,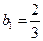 且
且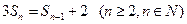 ;,
;,(Ⅰ)求数列
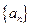 ,
,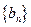 的通项公式;
的通项公式;(Ⅱ)若
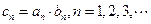 ,
,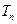 为数列
为数列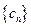 的前
的前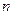 项和. 求证:
项和. 求证: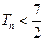 .
.解:(Ⅰ) 数列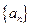 为等差数列,公差
为等差数列,公差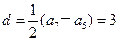 ,
,
易得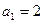
所以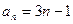 .…………2分
.…………2分
由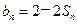 ,令
,令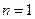 ,则
,则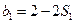 ,又
,又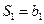 ,所以.
,所以.
 ,则
,则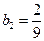 . …………………………………4分
. …………………………………4分
由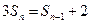
当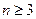 时,得
时,得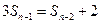 ,
,
两式相减得.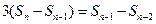 即
即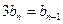
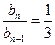 又
又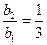
.所以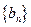 是以
是以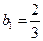 为首项,
为首项,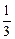 为公比的等比数列,
为公比的等比数列,
于是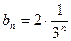 .………………………………………………………………6分
.………………………………………………………………6分
(Ⅱ)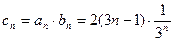 . …………………………………7分
. …………………………………7分
∴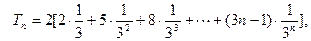
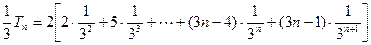
两式相减得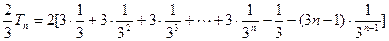 . ………10分
. ………10分
所以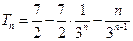 ……………11分
……………11分
从而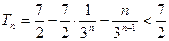 . …………………12分
. …………………12分
 为等差数列,公差
为等差数列,公差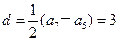 ,
,易得
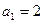
所以
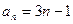 .…………2分
.…………2分由
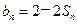 ,令
,令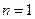 ,则
,则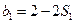 ,又
,又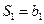 ,所以.
,所以. ,则
,则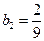 . …………………………………4分
. …………………………………4分由
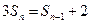
当
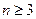 时,得
时,得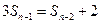 ,
,两式相减得.
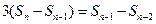 即
即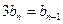
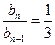 又
又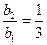
.所以
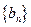 是以
是以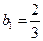 为首项,
为首项,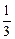 为公比的等比数列,
为公比的等比数列,于是
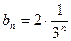 .………………………………………………………………6分
.………………………………………………………………6分(Ⅱ)
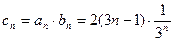 . …………………………………7分
. …………………………………7分∴
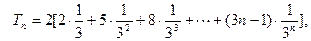
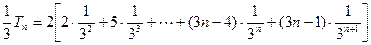
两式相减得
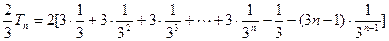 . ………10分
. ………10分所以
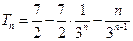 ……………11分
……………11分从而
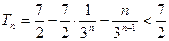 . …………………12分
. …………………12分略

练习册系列答案
 53随堂测系列答案
53随堂测系列答案
相关题目
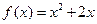 ,数列
,数列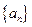 满足
满足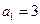 ,
,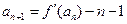 ,数列
,数列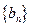 满足
满足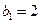 ,
,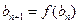 .
.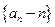 为等比数列.
为等比数列.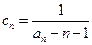 ,求证:
,求证: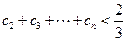 ;
;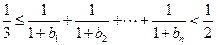
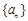 满足
满足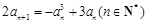 且
且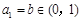
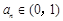 ;
;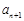 的大小;
的大小;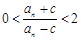 ,对一切
,对一切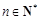 恒成立?若存在,则求出c的取值范围;若不存在,说明理由.
恒成立?若存在,则求出c的取值范围;若不存在,说明理由.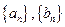 的各项均为正数,若对任意的正整数
的各项均为正数,若对任意的正整数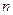 ,都有
,都有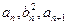 成等差数列,且
成等差数列,且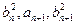 成等比数列.
成等比数列.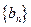 是等差数列;
是等差数列;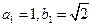 ,求数列
,求数列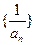 的前
的前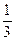 )是函数
)是函数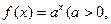 且
且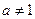 )的图象上一点,等比数列
)的图象上一点,等比数列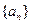 的前
的前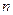 项和为
项和为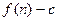 ,数列
,数列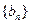
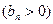 的首项为
的首项为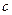 ,且前
,且前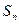 满足
满足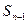 =
=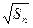 +
+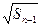 (
(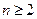 ).
).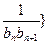 前
前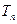 ,问
,问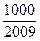 的最小正整数
的最小正整数

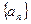 中,
中,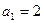 ,点
,点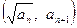 在函数
在函数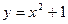 的图像上,数列
的图像上,数列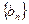 中,点
中,点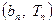 在直线
在直线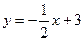 上,其中
上,其中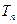 是数列
是数列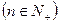 。
。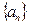 中,已知
中,已知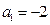 ,
,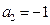 ,
,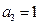 ,若对任意正整数
,若对任意正整数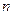 ,有
,有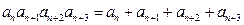 ,且
,且
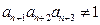 ,则该数列的前2010 项和
,则该数列的前2010 项和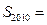 ( )
( )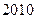 .
.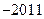 .
.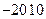 .
.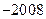 .
.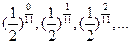 ,则使这个数列前
,则使这个数列前 项的积不小于
项的积不小于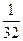 的最大正数
的最大正数