题目内容

3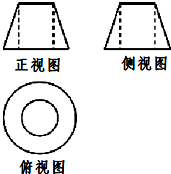．已知某几何体的三视图如图所示，正视图与侧视图都是上底为2，下底为4，底角为60°的等腰梯形，俯视图是直径分别为2和4的同心圆，则该几何体的表面积为（　　）
A．6πB．9πC．11πD．$（{9+2\sqrt{3}}）π$

分析 由三视图可以看出，本题中的几何体是一个圆台去掉一个圆柱，根据圆柱和圆台的表面积公式进行求解即可．

解答 解：由三视图知此几何体是一个圆台去掉一个圆柱，圆台的上底面半径为1，下底半径为2，高为$\sqrt{3}$，母线l=2，
圆柱的底面半径为1，高为$\sqrt{3}$，
则圆柱的侧面积为2$π×\sqrt{3}$=2$\sqrt{3}$π，
圆台的侧面积S=π（1+2）×2=6π，
底面面积S=4π-π=3π，
则该几何体的表面积为2$\sqrt{3}$π+6π+3π=（9+2$\sqrt{3}$）π，
故选：D

点评 本题主要考查几何体的表面积的计算，主要考查对三视图与实物图之间的关系，用三视图中的数据还原出实物图的数据是解决本题的关键．

练习册系列答案
相关题目
13．已知向量$\overrightarrow{a}$=（cosωx，sinωx），$\overrightarrow{b}$=（cosωx，$\sqrt{3}$cosωx），其中0＜ω＜2，设f（x）=$\overrightarrow{a}•\overrightarrow{b}$；
（1）若函数f（x）的周期为2π，求函数f（x）的单调增区间；
（2）若函数f（x）的图象的一条对称轴为x=$\frac{π}{6}$，求ω的值；
（3）若ω=1，且x∈[-$\frac{π}{6}$，$\frac{π}{6}$]时，求函数f（x）的最大值及最小值．
14．已知|$\overrightarrow{a}$|=1，|$\overrightarrow{b}$|=4，$\overrightarrow{a}$•（$\overrightarrow{b}$-$\overrightarrow{a}$）=1，则向量$\overrightarrow{a}$与$\overrightarrow{b}$的夹角为（　　）
A．$\frac{π}{3}$B．$\frac{π}{4}$C．$\frac{π}{6}$D．$\frac{π}{2}$
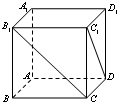11．正方体ABCD-A1B1C1D1中，异面直线B1C与C1D所成的角的大小为60°．
18．已知双曲线C：$\frac{x^2}{a^2}-\frac{y^2}{b^2}=1（a＞0，b＞0）$的离心率e=$\sqrt{3}$，且b=$\sqrt{2}$．
（Ⅰ）求双曲线C的方程；
（Ⅱ）若P为双曲线C上一点，双曲线C的左右焦点分别为E、F，且$\overrightarrow{PE}$•$\overrightarrow{PF}$=0，求△PEF的面积．
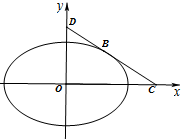8．已知椭圆C：$\frac{x^2}{a^2}+\frac{y^2}{b^2}$=1（a＞b＞0），离心率e=$\frac{{\sqrt{2}}}{2}$，且过$（\frac{{\sqrt{6}}}{2}，\frac{1}{2}）$．
（Ⅰ）求椭圆C的方程；
（Ⅱ）点B为椭圆C在第一象限中的任意一点，过B作C的切线l，l分别与x轴和y轴的正半轴交于C，D两点，求三角形OCD面积的最小值．
15．椭圆$\frac{x^2}{36}+\frac{y^2}{9}=1$的弦被点（4，2）平分，则此弦所在的直线方程是（　　）
A．x-2y=0B．x+2y=4C．2x+3y=14D．x+2y=8
12．已知数列{an}的首项${a_1}=\frac{3}{5}，{a_{n+1}}=\frac{{3{a_n}}}{{2{a_n}+1}}（n∈{N^*}）$，{an}的前n项和为Sn．
（1）求证：数列$\left\{{\frac{1}{a_n}-1}\right\}$是等比数列，并求数列{an}的通项公式；
（2）证明：对任意的$x＞0，{a_n}≥\frac{1}{1+x}-\frac{1}{{{{（1+x）}^2}}}（\frac{2}{3^n}-x），n∈{N^*}$．
（3）证明：${S_n}＞\frac{n^2}{n+1}$．
13．△ABC中，已知AB=2，BC=5，S△ABC=4，∠ABC=θ，则cosθ=$±\frac{3}{5}$．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网