题目内容
12.已知数列{an}的首项${a_1}=\frac{3}{5},{a_{n+1}}=\frac{{3{a_n}}}{{2{a_n}+1}}(n∈{N^*})$,{an}的前n项和为Sn.(1)求证:数列$\left\{{\frac{1}{a_n}-1}\right\}$是等比数列,并求数列{an}的通项公式;
(2)证明:对任意的$x>0,{a_n}≥\frac{1}{1+x}-\frac{1}{{{{(1+x)}^2}}}(\frac{2}{3^n}-x),n∈{N^*}$.
(3)证明:${S_n}>\frac{n^2}{n+1}$.
分析 (1)通过对${a_{n+1}}=\frac{{3{a_n}}}{{2{a_n}+1}}$取倒数、整理得数列$\left\{{\frac{1}{a_n}-1}\right\}$是首项为$\frac{2}{3}$、公比为$\frac{1}{3}$的等比数列,进而可得通项公式;
(2)通过令t=1+x,利用配方法即得结论;
(3)通过(2)可知${S_n}≥\frac{n}{1+x}-\frac{1}{{{{(1+x)}^2}}}(\frac{2}{3}+\frac{2}{3^2}+…+\frac{2}{3^n}-nx)$对任意的x>0恒成立,取$x=\frac{1}{n}(\frac{2}{3}+\frac{2}{3^2}+…+\frac{2}{3^n})$代入上式、放缩即得结论.
解答 证明:(1)通过对${a_{n+1}}=\frac{{3{a_n}}}{{2{a_n}+1}}$取倒数,
整理得:$\frac{1}{{{a_{n+1}}}}-1=\frac{1}{3}(\frac{1}{a_n}-1)$,
又∵a1=$\frac{3}{5}$,
∴$\frac{1}{a_1}-1=\frac{2}{3}≠0$,
∴数列$\left\{{\frac{1}{a_n}-1}\right\}$是首项为$\frac{2}{3}$、公比为$\frac{1}{3}$的等比数列,
∴${a_n}=\frac{3^n}{{{3^n}+2}}$;
(2)令t=1+x,则:
$\frac{1}{1+x}-\frac{1}{{{{(1+x)}^2}}}(\frac{2}{3^n}-x)=-(\frac{{2+{3^n}}}{3^n})\frac{1}{t^2}+\frac{2}{t}=-\frac{1}{a_n}•\frac{1}{t^2}+\frac{2}{t}$
=$-\frac{1}{a_n}{(\frac{1}{t}-{a_n})^2}+{a_n}≤{a_n}$;
(3)由(2)得,${S_n}≥\frac{n}{1+x}-\frac{1}{{{{(1+x)}^2}}}(\frac{2}{3}+\frac{2}{3^2}+…+\frac{2}{3^n}-nx)$对任意的x>0恒成立,
取$x=\frac{1}{n}(\frac{2}{3}+\frac{2}{3^2}+…+\frac{2}{3^n})$,代入上式,
得:${S_n}≥\frac{n}{{1+\frac{1}{n}(1-\frac{1}{3^n})}}>\frac{n}{{1+\frac{1}{n}}}=\frac{n^2}{n+1}$.
点评 本题考查等比数列的判定、数列的通项,考查运算求解能力,注意解题方法的积累,属于中档题.

| A. | [0,1] | B. | [1,2] | C. | [2,3] | D. | [3,4] |
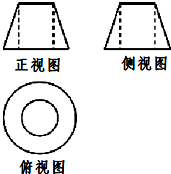 已知某几何体的三视图如图所示,正视图与侧视图都是上底为2,下底为4,底角为60°的等腰梯形,俯视图是直径分别为2和4的同心圆,则该几何体的表面积为( )
已知某几何体的三视图如图所示,正视图与侧视图都是上底为2,下底为4,底角为60°的等腰梯形,俯视图是直径分别为2和4的同心圆,则该几何体的表面积为( )| A. | 6π | B. | 9π | C. | 11π | D. | $({9+2\sqrt{3}})π$ |
| A. | $\frac{2}{3}$ | B. | $\frac{5}{48}$ | C. | $\frac{4}{5}$ | D. | $\frac{5}{16}$ |
| 男性 | 女性 | 合计 | |
| 反感 | a=10 | b= | |
| 不反感 | c= | d=8 | |
| 合计 | 30 |
(1)请将上面的2×2列联表补充完整(在答题卡上直接填写结果,不需要写求解过程),并据此资料分析反感“中国式过马路”与性别是否有关?
(2)若从这30人中的女性路人中随机抽取2人参加一活动,记反感“中国式过马路”的人数为X,求X的分布列和数学期望.
参考数据和公式:
2×2列联表K2公式:K2=$\frac{n(ad-bc)^{2}}{(a+b)(c+d)(a+c)(b+d)}$,K2的临界值表:
| P(K2≥k) | 0.50 | 0.40 | 0.25 | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| k | 0.455 | 0.708 | 1.323 | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
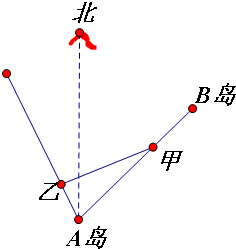 已知海岛B在海岛A的北偏东45°方向上,A、B相距10海里,小船甲从海岛B以2海里/小时的速度沿直线向海岛A移动,同时小船乙从海岛A出发沿北偏15°方向也以2海里/小时的速度移动
已知海岛B在海岛A的北偏东45°方向上,A、B相距10海里,小船甲从海岛B以2海里/小时的速度沿直线向海岛A移动,同时小船乙从海岛A出发沿北偏15°方向也以2海里/小时的速度移动