题目内容
8. 已知椭圆C:$\frac{x^2}{a^2}+\frac{y^2}{b^2}$=1(a>b>0),离心率e=$\frac{{\sqrt{2}}}{2}$,且过$(\frac{{\sqrt{6}}}{2},\frac{1}{2})$.
已知椭圆C:$\frac{x^2}{a^2}+\frac{y^2}{b^2}$=1(a>b>0),离心率e=$\frac{{\sqrt{2}}}{2}$,且过$(\frac{{\sqrt{6}}}{2},\frac{1}{2})$.(Ⅰ)求椭圆C的方程;
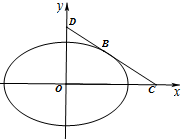
(Ⅱ)点B为椭圆C在第一象限中的任意一点,过B作C的切线l,l分别与x轴和y轴的正半轴交于C,D两点,求三角形OCD面积的最小值.
分析 (1)通过将$(\frac{{\sqrt{6}}}{2},\frac{1}{2})$代入椭圆C方程并联立e=$\frac{c}{a}$=$\frac{\sqrt{{a}^{2}-{b}^{2}}}{a}$=$\frac{{\sqrt{2}}}{2}$,进而计算可得结论;
(2)通过设l:y=kx+b(k<0)并与椭圆方程联立,利用△=0可知b2=1+2k2,进而计算可得结论.
解答 解:(1)∵椭圆C:$\frac{x^2}{a^2}+\frac{y^2}{b^2}$=1(a>b>0)过$(\frac{{\sqrt{6}}}{2},\frac{1}{2})$,
∴$\frac{3}{2{a}^{2}}+\frac{1}{4{b}^{2}}=1$,
又∵离心率e=$\frac{c}{a}$=$\frac{\sqrt{{a}^{2}-{b}^{2}}}{a}$=$\frac{{\sqrt{2}}}{2}$,
∴a2=2,b2=1,
∴椭圆C的方程为:$\frac{x^2}{2}+{y^2}=1$;
(2)设l:y=kx+b(k<0),
联立$\left\{\begin{array}{l}{y=kx+b}\\{\frac{{x}^{2}}{2}+{y}^{2}=1}\end{array}\right.$,消去y整理得:($\frac{1}{2}$+k)x2+2kbx+b2+1=0,
令△=$4{k}^{2}{•b}^{2}-4•(\frac{1}{2}+k)•({b}^{2}+1)$=0,则b2=1+2k2,
∴${S_{△OCD}}=\frac{1}{2}•(-\frac{b}{k})•b=-\frac{b^2}{2k}=-\frac{{1+2{k^2}}}{2k}=\frac{1}{2}[{\frac{1}{-k}+(-2k)}]≥\sqrt{2}$,
当且仅当$\frac{1}{-k}=-2k$,即$k=-\frac{{\sqrt{2}}}{2}$时取等号,
∴三角形OCD的面积的最小值为$\sqrt{2}$.
点评 本题是一道直线与圆锥曲线的综合题,考查运算求解能力,注意解题方法的积累,属于中档题.

 口算题天天练系列答案
口算题天天练系列答案 电视传媒公司为了解某地区观众对某体育节目的收视情况,随机抽取了100名观众进行调查,其中女性有55名,下面是根据调查结果绘制的观众日均收看该体育节目时间的频率分布直方图:将日均收看该体育节目时间不低于40分钟的观众称为“体育迷”.
电视传媒公司为了解某地区观众对某体育节目的收视情况,随机抽取了100名观众进行调查,其中女性有55名,下面是根据调查结果绘制的观众日均收看该体育节目时间的频率分布直方图:将日均收看该体育节目时间不低于40分钟的观众称为“体育迷”.(1)根据已知条件完成下面的2×2列联表,并据此资料你是否认为“体育迷”与性别有关?
| 非体育迷 | 体育迷 | 合计 | |
| 男 | |||
| 女 | 10 | 55 | |
| 合计 |
| P(K2≥k) | 0.05 | 0.01 |
| k | 3.841 | 6.635 |
 已知某几何体的三视图如图所示,正视图与侧视图都是上底为2,下底为4,底角为60°的等腰梯形,俯视图是直径分别为2和4的同心圆,则该几何体的表面积为( )
已知某几何体的三视图如图所示,正视图与侧视图都是上底为2,下底为4,底角为60°的等腰梯形,俯视图是直径分别为2和4的同心圆,则该几何体的表面积为( )| A. | 6π | B. | 9π | C. | 11π | D. | $({9+2\sqrt{3}})π$ |
| 男性 | 女性 | 合计 | |
| 反感 | a=10 | b= | |
| 不反感 | c= | d=8 | |
| 合计 | 30 |
(1)请将上面的2×2列联表补充完整(在答题卡上直接填写结果,不需要写求解过程),并据此资料分析反感“中国式过马路”与性别是否有关?
(2)若从这30人中的女性路人中随机抽取2人参加一活动,记反感“中国式过马路”的人数为X,求X的分布列和数学期望.
参考数据和公式:
2×2列联表K2公式:K2=$\frac{n(ad-bc)^{2}}{(a+b)(c+d)(a+c)(b+d)}$,K2的临界值表:
| P(K2≥k) | 0.50 | 0.40 | 0.25 | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| k | 0.455 | 0.708 | 1.323 | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
 一个几何体的三视图如所示,则这个几何体的表面积为2$\sqrt{2}$.
一个几何体的三视图如所示,则这个几何体的表面积为2$\sqrt{2}$. 已知海岛B在海岛A的北偏东45°方向上,A、B相距10海里,小船甲从海岛B以2海里/小时的速度沿直线向海岛A移动,同时小船乙从海岛A出发沿北偏15°方向也以2海里/小时的速度移动
已知海岛B在海岛A的北偏东45°方向上,A、B相距10海里,小船甲从海岛B以2海里/小时的速度沿直线向海岛A移动,同时小船乙从海岛A出发沿北偏15°方向也以2海里/小时的速度移动