题目内容
14.已知|$\overrightarrow{a}$|=1,|$\overrightarrow{b}$|=4,$\overrightarrow{a}$•($\overrightarrow{b}$-$\overrightarrow{a}$)=1,则向量$\overrightarrow{a}$与$\overrightarrow{b}$的夹角为( )| A. | $\frac{π}{3}$ | B. | $\frac{π}{4}$ | C. | $\frac{π}{6}$ | D. | $\frac{π}{2}$ |
分析 展开单项式乘多项式,代入平面向量的数量积公式,则向量$\overrightarrow{a}$与$\overrightarrow{b}$的夹角可求.
解答 解:由$\overrightarrow{a}$•($\overrightarrow{b}$-$\overrightarrow{a}$)=1,得$\overrightarrow{a}•\overrightarrow{b}-|\overrightarrow{a}{|}^{2}=1$,
即$|\overrightarrow{a}|•|\overrightarrow{b}|cos<\overrightarrow{a},\overrightarrow{b}>-|\overrightarrow{a}{|}^{2}=1$,
∵|$\overrightarrow{a}$|=1,|$\overrightarrow{b}$|=4,∴4cos<$\overrightarrow{a},\overrightarrow{b}$>=2,即cos<$\overrightarrow{a},\overrightarrow{b}$>=$\frac{1}{2}$,
又<$\overrightarrow{a},\overrightarrow{b}$>∈[0,π],
∴向量$\overrightarrow{a}$与$\overrightarrow{b}$的夹角为$\frac{π}{3}$.
故选:A.
点评 本题考查平面向量的数量积运算,考查了向量的夹角,是基础题.

练习册系列答案
相关题目
2.函数f(x)=x3+x-3的实数解落在的区间是( )
| A. | [0,1] | B. | [1,2] | C. | [2,3] | D. | [3,4] |
9.已知向量$\overrightarrow{a}$=(1,-2,2),$\overrightarrow{b}$=(2,-1,2),那么向量$\overrightarrow{a}$,$\overrightarrow{b}$的夹角等于( )
| A. | -arccos$\frac{8}{9}$ | B. | π-arccos$\frac{8}{9}$ | C. | arccos$\frac{8}{9}$ | D. | π+arccos$\frac{8}{9}$ |
3.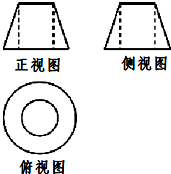 已知某几何体的三视图如图所示,正视图与侧视图都是上底为2,下底为4,底角为60°的等腰梯形,俯视图是直径分别为2和4的同心圆,则该几何体的表面积为( )
已知某几何体的三视图如图所示,正视图与侧视图都是上底为2,下底为4,底角为60°的等腰梯形,俯视图是直径分别为2和4的同心圆,则该几何体的表面积为( )
 已知某几何体的三视图如图所示,正视图与侧视图都是上底为2,下底为4,底角为60°的等腰梯形,俯视图是直径分别为2和4的同心圆,则该几何体的表面积为( )
已知某几何体的三视图如图所示,正视图与侧视图都是上底为2,下底为4,底角为60°的等腰梯形,俯视图是直径分别为2和4的同心圆,则该几何体的表面积为( )| A. | 6π | B. | 9π | C. | 11π | D. | $({9+2\sqrt{3}})π$ |
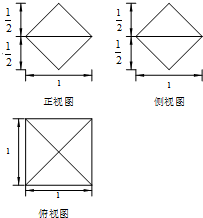 一个几何体的三视图如所示,则这个几何体的表面积为2$\sqrt{2}$.
一个几何体的三视图如所示,则这个几何体的表面积为2$\sqrt{2}$.