题目内容
【题目】有一容积为![]() 的正方体容器
的正方体容器![]() ,在棱
,在棱![]() 、
、![]() 和面对角线
和面对角线![]() 的中点各有一小孔
的中点各有一小孔![]() 、
、![]() 、
、![]() ,若此容器可以任意放置,则其可装水的最大容积是( )
,若此容器可以任意放置,则其可装水的最大容积是( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
【答案】C
【解析】
分别讨论水面过直线![]() 、
、![]() 、
、![]() 时从正方体截去的几何体体积的最小值,即可得出此容器可装水的最大容积.
时从正方体截去的几何体体积的最小值,即可得出此容器可装水的最大容积.
当水面过直线![]() 时,如下图所示,
时,如下图所示,
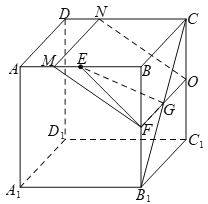
水面截去正方体![]() 所得几何体为三棱柱
所得几何体为三棱柱![]() ,
,
当点![]() 在水面上方或水面上时,容器中的水不会漏,且当点
在水面上方或水面上时,容器中的水不会漏,且当点![]() 与点
与点![]() 重合时,截去的几何体体积最小为
重合时,截去的几何体体积最小为![]() ;
;
当水面过直线![]() 时,如下图所示,
时,如下图所示,
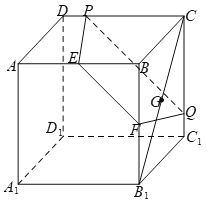
水面截去正方体![]() 所得几何体为三棱台
所得几何体为三棱台![]() ,
,
当点![]() 在水面上方或水面上时,容器中的水不会漏,且当点
在水面上方或水面上时,容器中的水不会漏,且当点![]() 在直线
在直线![]() 上时,截去的几何体为三棱柱,且体积最小为
上时,截去的几何体为三棱柱,且体积最小为![]() ;
;
当水面过直线![]() 时,如下图所示,
时,如下图所示,
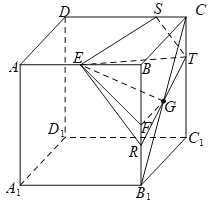
当点![]() 在水面上方或水面上时,容器中的水不会漏,此时水面截去正方体
在水面上方或水面上时,容器中的水不会漏,此时水面截去正方体![]() 所得几何体为
所得几何体为![]() ,且直线
,且直线![]() 过点
过点![]() ,易知梯形
,易知梯形![]() 的面积为正方形
的面积为正方形![]() 面积的一半,此时,几何体
面积的一半,此时,几何体![]() 的体积为
的体积为![]() .
.
当![]() 与直线
与直线![]() 重合时,如下图所示,
重合时,如下图所示,
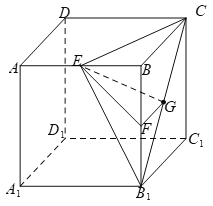
此时,点![]() 在水面上方,容器不会漏水,水面截去正方体
在水面上方,容器不会漏水,水面截去正方体![]() 所得几何体为三棱锥
所得几何体为三棱锥![]() ,
,
该三棱锥的体积为![]() .
.
综上可知,水面截去截去正方体![]() 所得几何体体积的最小值为
所得几何体体积的最小值为![]() .
.
因此,该容器可装水的最大容积是![]() .
.
故选:C.

练习册系列答案
 课堂全解字词句段篇章系列答案
课堂全解字词句段篇章系列答案 步步高口算题卡系列答案
步步高口算题卡系列答案
相关题目
【题目】王先生购买了一部手机,欲使用中国移动“神州行”卡或加入联通的![]() 网,经调查其收费标准见下表:(注:本地电话费以分为计费单位,长途话费以秒为计费单位.)
网,经调查其收费标准见下表:(注:本地电话费以分为计费单位,长途话费以秒为计费单位.)
网络 | 月租费 | 本地话费 | 长途话费 |
甲:联通 |
|
|
|
乙:移动“神州行” | 无 |
|
|
若王先生每月拨打本地电话的时间是拨打长途电话时间的![]() 倍,若要用联通
倍,若要用联通![]() 应最少打多长时间的长途电话才合算.( )
应最少打多长时间的长途电话才合算.( )
A.![]() 秒B.
秒B.![]() 秒C.
秒C.![]() 秒D.
秒D.![]() 秒
秒