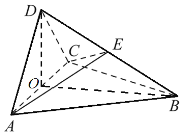
题目内容

【题目】已知椭圆经过点离心率.

（Ⅰ）求椭圆的方程；

（Ⅱ）经过椭圆左焦点的直线(不经过点且不与轴重合)与椭圆交于两点，与直线:交于点，记直线的斜率分别为.则是否存在常数，使得向量 共线？若存在求出的值；若不存在，说明理由.

【答案】（1）；（2）2.

【解析】

（1）根据椭圆经过点，离心率，结合性质 ，列出关于 、 、的方程组，求出 、，即可得结果；（2）直线的方程为， 代入椭圆方程整理得，求得的坐标为，求出 ,利用韦达定理化简可得，从而可得结果.

（1）由在椭圆上， .①

由已知得，

又， .②

②代入①解得.

椭圆的方程为.

（2）假设存在常数，使得向量共线，

，即.

由题意可设的斜率为，

则直线的方程为，③

代入椭圆方程并整理，得，

设，则有

，.④

在方程③中令得，的坐标为.

从而，，.

, ⑤

④代入⑤得，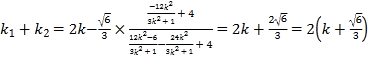

又， .

故存在常数符合题意.

练习册系列答案
相关题目

【题目】已知函数，.

（1）讨论函数的单调性；

（2）当a=1时，若关于的不等式恒成立，求实数的取值范围．

【题目】已知函数（为常数，是自然对数的底数），曲线在点处的切线与轴平行.

（Ⅰ）求的值；

（Ⅱ）求的单调区间；

（Ⅲ）设,其中为的导函数.证明：对任意.

【题目】已知数列{an}满足，且．

(1)求证：数列是等差数列，并求出数列的通项公式；

(2)求数列的前项和.

【题目】设椭圆的离心率，抛物线的焦点恰好是椭圆的右焦点．

（1）求椭圆的标准方程；

（2）过点作两条斜率都存在的直线，设与椭圆交于两点，与椭圆交于两点，若是与的等比中项，求的最小值．

【题目】如图，四面体ABCD中，平面DAC⊥底面ABC，，AD＝CD＝，O是AC的中点，E是BD的中点．

（1）证明：DO⊥底面ABC；

（2）求二面角D-AE-C的余弦值．

【题目】某校100名学生期中考试语文成绩的频率分布直方图如图所示，其中成绩分组区间是：[50,60)，[60,70)，[70,80)，[80,90)，[90,100]．

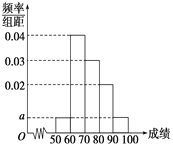
(1)求图中a的值；

(2)根据频率分布直方图，估计这100名学生语文成绩的平均分；

(3)若这100名学生语文成绩某些分数段的人数(x)与数学成绩相应分数段的人数(y)之比如下表所示，求数学成绩在[50,90)之外的人数.

分数段

[50,60)

[60,70)

[70,80)

[80,90)

x∶y

1∶1

2∶1

3∶4

4∶5

【题目】已知椭圆：的离心率为，且与抛物线交于，两点， （为坐标原点）的面积为．

（1）求椭圆的方程；

（2）如图，点为椭圆上一动点（非长轴端点），为左、右焦点，的延长线与椭圆交于点，的延长线与椭圆交于点，求面积的最大值．

【题目】某城市为鼓励人们绿色出行，乘坐地铁，地铁公司决定按照乘客经过地铁站的数量实施分段优惠政策，不超过站的地铁票价如下表：

乘坐站数

票价（元）

现有甲、乙两位乘客同时从起点乘坐同一辆地铁，已知他们乘坐地铁都不超过站.甲、乙乘坐不超过站的概率分别为， ；甲、乙乘坐超过站的概率分别为， .

（1）求甲、乙两人付费相同的概率；

（2）设甲、乙两人所付费用之和为随机变量，求的分布列和数学期望.

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网