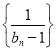Question

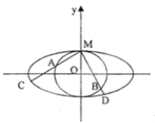
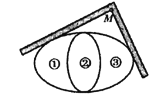
【题目】如图所示，取同离心率的两个椭圆成轴对称内外嵌套得一个标志，为美观考虑，要求图中标记的①、②、③）三个区域面积彼此相等.（已知：椭圆面积为圆周率与长半轴、短半轴长度之积，即椭圆面积为）

（1）求椭圆的离心率的值；

（2）已知外椭圆长轴长为6，用直角角尺两条直角边内边缘与外椭圆相切，移动角尺绕外椭圆一周，得到由点M生成的轨迹将两椭圆围起来，整个标志完成.请你建立合适的坐标系，求出点M的轨迹方程.

Answer 1

【答案】（1）

（2）

【解析】

（1）建立如图平面直角坐标系,由对称性只需，所以，化简即得椭圆的离心率的值；（2）同（1）建立如图平面直角坐标系，先求出外椭圆方程为，设点，根据直线和椭圆相切得到，即得点M的轨迹方程.

（1）建立如图平面直角坐标系,

设外椭圆的方程为，因为内外椭圆有相同的离心率且共轴，

所以内椭圆的方程为.

图中标记的①、②、③三个区域面积彼此相等，由对称性只需，

即即

所以.

（2）同（1）建立如图平面直角坐标系，由于外椭圆长轴为6，

所以，，所以，.

所以外椭圆方程为.

设点，切线方程为代入椭圆方程得：

[

直线和椭圆相切

化简得

因为两条切线互相垂直，所以，

即，

即

当两切线与坐标轴垂直时，四点也满足方程，

所以轨迹方程为.