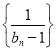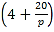Question

【题目】将函数的图象向右平移个单位长度后得到函数的图象,分别是的极值点,且有,则函数 ( )

A.在区间上单调递增B.在区间上单调递增

C.在区间上单调递减D.在区间上单调递减

Answer 1

【答案】D

【解析】

先得到的一个极值大点，然后根据，得到的一个极大值点或极小值点，分别得到，再得到的解析式，再分别求出其单调区间，判断四个选项是否符合，从而得到答案.

，可知是其一个极值点，

，

因为分别是的极值点，且有，

所以的一个极大值点为，

或者的一个极小值点为，

①的一个极大值点为时，

代入到，得，

即，，

即，，

因为，所以，，

所以，

，，

即，，

所以的单调递增区间为，，

，，

即，，

所以的单调递减区间为，，

因此可得，在区间上单调递减，选项D符合.

②的一个极小值点为时，

代入到，得，

即，，

即，，

因为，所以，，

所以，

，，

即，，

所以的单调递增区间为，，

，，

即，，

所以的单调递减区间为，，

所以这种情况下，没有选项符合.

故选：D.