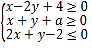Question

【题目】已知函数的周期为，图象的一个对称中心为.将函数图象上所有点的横坐标伸长到原来的2倍(纵坐标不变)，再将所得到的图象向右平移个单位长度后得到函数的图象.

(1)求函数与的解析式.

(2)定义:当函数取得最值时,函数图象上对应的点称为函数的最值点,如果函数的图象上至少有一个最大值点和一个最小值点在圆的内部或圆周上，求k的取值范围.

Answer 1

【答案】（1）,;（2）.

【解析】

(1)由函数的周期为可得,再由对称中心为可得值,由函数图象变换和诱导公式可得所求的解析式.

(2)由三角函数的知识可得与原点距离最近的最大值和最小值点分别是点和,由题意结合图象可得,解不等式可得的范围.

（1）∵函数的周期为,∴.

又∵曲线的一个对称中心为，

∴，,可得，∴.

将函数图象上所有点的横坐标伸长到原来的2倍(纵坐标不变)后可得的图象，再将的图象向右平移个单位长度后得到函数的图象,

由诱导公式化简可得.

(2)∵函数在时取得最大值或最小值，

故，其中.

与原点距离最近的最大值和最小值点分别是点和，

于是有，解不等式可得.