题目内容
(本题满分14分)
设数列 的前n项和为
的前n项和为 ,且
,且 ,其中p是不为零的常数.
,其中p是不为零的常数.
(1)证明:数列 是等比数列;
是等比数列;
(2)当p=3时,若数列 满足
满足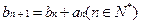 ,
, ,求数列
,求数列 的通项公式.
的通项公式.
设数列
 的前n项和为
的前n项和为 ,且
,且 ,其中p是不为零的常数.
,其中p是不为零的常数.(1)证明:数列
 是等比数列;
是等比数列;(2)当p=3时,若数列
 满足
满足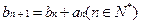 ,
, ,求数列
,求数列 的通项公式.
的通项公式.(1)证:因为Sn=4an– p(n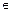 N*),则Sn – 1 = 4an – 1 – p(n
N*),则Sn – 1 = 4an – 1 – p(n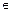 N*,n
N*,n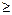 2),
2),
所以当n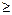 2时,
2时,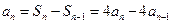 ,整理得
,整理得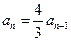 . 5分
. 5分
由Sn=4an– p,令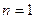 ,得
,得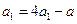 ,解得
,解得 .
.
所以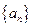 是首项为
是首项为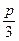 ,公比为
,公比为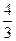 的等比数列. 7分
的等比数列. 7分
(2)解:因为a1=1,则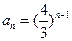 ,
,
由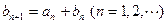 ,得
,得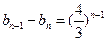 , 9分
, 9分
当n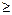 2时,由累加得
2时,由累加得
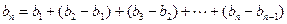 =
=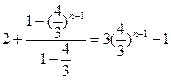 ,
,
当n = 1时,上式也成立. 14分
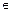 N*),则Sn – 1 = 4an – 1 – p(n
N*),则Sn – 1 = 4an – 1 – p(n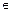 N*,n
N*,n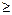 2),
2),所以当n
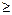 2时,
2时,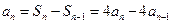 ,整理得
,整理得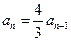 . 5分
. 5分由Sn=4an– p,令
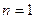 ,得
,得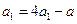 ,解得
,解得 .
.所以
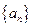 是首项为
是首项为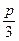 ,公比为
,公比为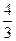 的等比数列. 7分
的等比数列. 7分(2)解:因为a1=1,则
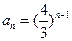 ,
,由
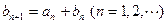 ,得
,得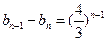 , 9分
, 9分当n
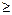 2时,由累加得
2时,由累加得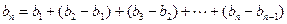 =
=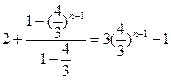 ,
,当n = 1时,上式也成立. 14分
略

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
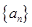 的前
的前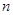 项和为
项和为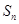 ,若
,若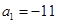 ,
,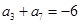 ,则当
,则当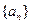 为等比数列,
为等比数列,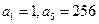 ;
;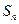 为等差数列
为等差数列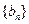 的前n项和,
的前n项和,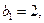
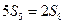 .
.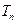
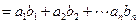 ,求
,求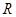 上的函数
上的函数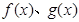 满足
满足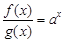 ,且
,且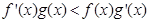 ,
,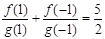 ,若有穷数列
,若有穷数列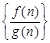 (
(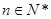 )的前
)的前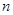 项和等于
项和等于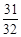 ,则n等于
,则n等于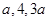 为等差数列的连续三项,则
为等差数列的连续三项,则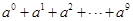 的值为 ( )
的值为 ( )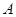
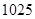
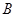
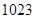
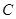
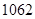
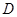
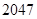

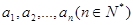 满足条件:
满足条件: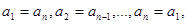
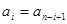 ,
,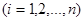 我们称其为“对称数列”.例如:数列1,2,3,3,2,1 和数列1,2,3,4,3,2,1都为 “对称数列”。已知数列
我们称其为“对称数列”.例如:数列1,2,3,3,2,1 和数列1,2,3,4,3,2,1都为 “对称数列”。已知数列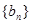 是项数不超过
是项数不超过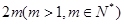 的“对称数列”,并使得
的“对称数列”,并使得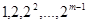 依次为该数列中连续的前
依次为该数列中连续的前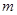 项,则数列
项,则数列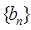 的前2009项和
的前2009项和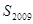 所有可能的取值的序号为 ( )
所有可能的取值的序号为 ( )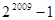 ②
②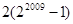 ③
③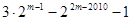 ④
④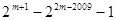
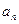 }满足
}满足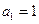 ,且
,且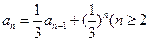 ,且
,且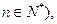 则数列{
则数列{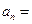
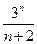
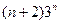
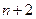
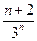
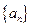 是等差数列,其中
是等差数列,其中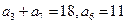 .
.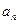 ;
;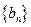 满足
满足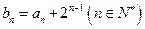 ,求数列
,求数列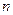 项和
项和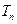 .
.