题目内容
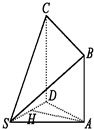
设三棱锥s-ABC的顶点P在底面的射影S′(在△ABC内部)到三个侧面的距离相等,则S′是△ABC的( )
| A.外心 | B.垂心 | C.内心 | D.重心 |
如图,S'在三个侧面上的射影分别为E,F,G;连接SE,SF,SG,延长线交底面于,P,Q,R,
∵S'到三个侧面距离相等
∴S'E=S'F=S'G
∴SE=SF=SG
S'P=S'Q=S'R EQ=FP=GR (先证出相等)
∵AB⊥S'S AB⊥S'F
∴AB⊥△SPS'
∴AB⊥S'P
同理证得BC⊥S'Q AC⊥S'R (又证出垂直)
所以S’是底面三角形的内心
故选C.
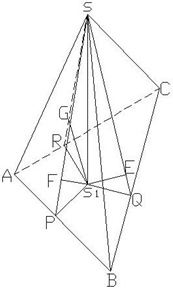
∵S'到三个侧面距离相等
∴S'E=S'F=S'G
∴SE=SF=SG
S'P=S'Q=S'R EQ=FP=GR (先证出相等)
∵AB⊥S'S AB⊥S'F
∴AB⊥△SPS'
∴AB⊥S'P
同理证得BC⊥S'Q AC⊥S'R (又证出垂直)
所以S’是底面三角形的内心
故选C.


练习册系列答案
相关题目