题目内容

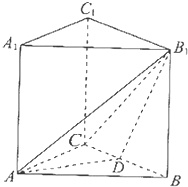
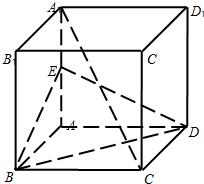
在正方体ABCD-A1B1C1D1中，E是AA1的中点．
（1）求CAl与底面ABCD所成角的正切值；
（2）证明A1C∥平面BDE．
（1）在正方体ABCD-A1B1C1D1中，由于AA1⊥底面ABCD，故∠A1CA即为CAl与底面ABCD所成角．
设正方体的棱长等于1，则 AA1=1，AC=
2
，Rt△A1CA中，tan∠A1CA=
AA1
AC
=
1
2
．
（2）证明：设AC和BD交与点O，则O是AC的中点．再由E是AA1的中点可得EO是△A1CA的中位线，∴EO∥AC．
而EO?平面BDE，A1C不在平面BDE 内，∴A1C∥平面BDE．
练习册系列答案
相关题目
设三棱锥s-ABC的顶点P在底面的射影S′（在△ABC内部）到三个侧面的距离相等，则S′是△ABC的（　　）
A．外心B．垂心C．内心D．重心
如图，在正三棱柱ABC-A1B1C1中，BC=BB1，点D是BC的中点．
（I）求证：A1C1∥平面AB1C；
（Ⅱ）求证：△AB1D为直角三角形；
（Ⅲ）若三棱锥B1-ACD的体积为
3
3
，求棱BB1的长．
如图所示，PD⊥底面ABCD，四边形ABCD是正方形，PD=DC，E是PC的中点．
（1）证明：PA∥平面BDE；
（2）证明：平面ADE⊥平面PBC；
（3）求直线AE与平面ABCD所成角的余弦值．
如图甲，在等边三角形ABC中，D，E分别是AB，AC边上的点，AD=AE，F是BC上的点，AF与DE交于点G，将△ABF沿AF折起，得到如图乙所示的三棱锥A-BCF，证明：DE∥平面BCF．
已知直三棱柱ABC-A1B1C1中，AB⊥AC，AB=AC=AA1，D，E，F分别为AB1，CC1，BC的中点．
（1）求证：DE∥平面ABC；
（2）求证：B1F⊥平面AEF．
在正四面体PABC中，D，E，F分别是棱AB，BC，CA的中点．给出下面四个结论：
①BC∥平面PDF；②DF⊥平面PAE；③平面PDF⊥平面ABC；④平面PAE⊥平面ABC，
其中所有不正确的结论的序号是______．
如图，四棱锥S-ABCD中，底面ABCD为平行四边形，E是SA上一点，试探求点E的位置，使SC∥平面EBD，并证明．
（文科做）已知平面α∥面β，AB、CD为异面线段，AB?α，CD?β，且AB=a，CD=b，AB与CD所成的角为θ，平面γ∥面α，且平面γ与AC、BC、BD、AD分别相交于点M、N、P、Q．
（1）若a=b，求截面四边形MNPQ的周长；
（2）求截面四边形MNPQ面积的最大值．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网