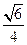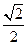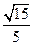题目内容
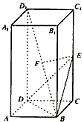
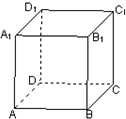
如图,在正方体ABCD-A1B1C1D1中,AB=2.则点A到面A1DCB1的距离是( )
A.
| B.
| C.
| D.2 |

如图所示,连接A1D,AD1,B1C. 设AD1∩A1D=O.
设AD1∩A1D=O.
由正方体可得CD⊥侧面ADD1A1,四边形ADD1A1是正方形.
∴CD⊥AD1,A1D⊥AD1.
又A1D∩DC=D.
∴AD1⊥平面A1B1CD.
∴AO即为点A到平面A1DCB1的距离.
∴AO=
AD1=
=
.
故选B.
 设AD1∩A1D=O.
设AD1∩A1D=O.由正方体可得CD⊥侧面ADD1A1,四边形ADD1A1是正方形.
∴CD⊥AD1,A1D⊥AD1.
又A1D∩DC=D.
∴AD1⊥平面A1B1CD.
∴AO即为点A到平面A1DCB1的距离.
∴AO=
| 1 |
| 2 |
2
| ||
| 2 |
| 2 |
故选B.

练习册系列答案
相关题目
 ,
,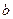 平面
平面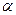 ,且
,且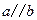 ,
,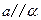 ,
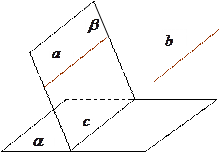
, .
.
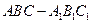 的棱长都是
的棱长都是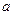 ,那么
,那么 与面
与面 所成角的正弦值为
所成角的正弦值为