题目内容
(12分)已知{an}是一个公差大于0的等差数列,且满足a3a6=55,a2+a7=16。
(1)求数列{an}的通项公式;
(2)若数列{an}和数列{bn}满足等式:an=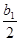 +
+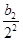 +
+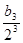 +……+
+……+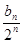 ,(n
,(n N+),
N+),
求数列{bn}的前n项和Sn。
(1)求数列{an}的通项公式;
(2)若数列{an}和数列{bn}满足等式:an=
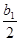 +
+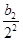 +
+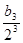 +……+
+……+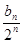 ,(n
,(n N+),
N+),求数列{bn}的前n项和Sn。
(1)an=a3+(n-3)d=2n-1;(2)当n=1时,S1=b1=2
当n≥2时,Sn=b1+b2+b3+……+bn=2+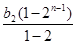 =2n+2-6
=2n+2-6
当n≥2时,Sn=b1+b2+b3+……+bn=2+
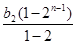 =2n+2-6
=2n+2-6求一个数列的前n项和应该先求出数列的通项,利用通项的特点,然后选择合适的求和的方法.
(1)将已知条件a3a6=55,a2+a7=16,利用等差数列的通项公式用首项与公差表示,列出方程组,求出首项与公差,进一步求出数列{an}的通项公式
(2)将已知等式仿写出一个新等式,两个式子相减求出数列{bn}的通项,利用等比数列的前n项和公式求出数列{bn}的前n项和Sn.
解:(1)由等差数列的性质得:a2+a7=a3+a6
∴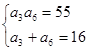 ,解得:
,解得: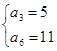 或
或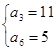
∵{an}的公差大于0 ∴{an}单增数列
∴a3=5,a6=11 ∴公差d=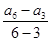 =
=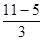 =2
=2
∴an=a3+(n-3)d=2n-1
(2)当n=1时,a1=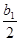 ∴b1=2
∴b1=2
当n≥2时,an=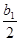 +
+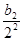 +
+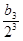 +…+
+…+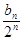
an-1=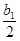 +
+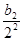 +
+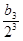 +…+
+…+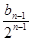
两式相减得:an-a n-1=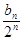
∴bn=2n+1,n≥2

∴当n=1时,S1=b1=2
当n≥2时,Sn=b1+b2+b3+……+bn
=2+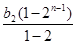 =2n+2-6
=2n+2-6
(1)将已知条件a3a6=55,a2+a7=16,利用等差数列的通项公式用首项与公差表示,列出方程组,求出首项与公差,进一步求出数列{an}的通项公式
(2)将已知等式仿写出一个新等式,两个式子相减求出数列{bn}的通项,利用等比数列的前n项和公式求出数列{bn}的前n项和Sn.
解:(1)由等差数列的性质得:a2+a7=a3+a6
∴
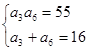 ,解得:
,解得: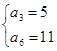 或
或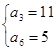
∵{an}的公差大于0 ∴{an}单增数列
∴a3=5,a6=11 ∴公差d=
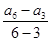 =
=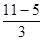 =2
=2∴an=a3+(n-3)d=2n-1
(2)当n=1时,a1=
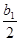 ∴b1=2
∴b1=2当n≥2时,an=
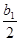 +
+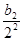 +
+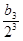 +…+
+…+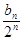
an-1=
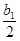 +
+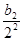 +
+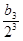 +…+
+…+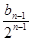
两式相减得:an-a n-1=
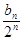
∴bn=2n+1,n≥2

∴当n=1时,S1=b1=2
当n≥2时,Sn=b1+b2+b3+……+bn
=2+
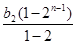 =2n+2-6
=2n+2-6
练习册系列答案
 名师指导期末冲刺卷系列答案
名师指导期末冲刺卷系列答案
相关题目
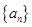 满足:
满足: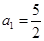 ,且
,且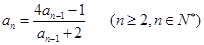
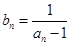 ,证明数列
,证明数列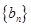 是等差数列;(2)求数列
是等差数列;(2)求数列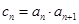 ,
,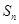 为数列
为数列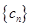 的前
的前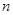 项和,证明
项和,证明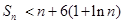 .
.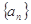 中,若
中,若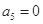 ,则有等式
,则有等式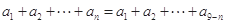
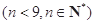 成立.类比上述性质:在等比数列
成立.类比上述性质:在等比数列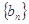 中,若
中,若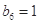 ,则有等式 成立.
,则有等式 成立.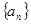 的前n项的和Sn = 2n2-n+1,则an=
的前n项的和Sn = 2n2-n+1,则an= 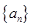 和
和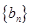 的前n项和分别为
的前n项和分别为 ,且
,且 ,则使得
,则使得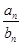 为整数的正整数n的个数是___
为整数的正整数n的个数是___ 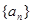 是等差数列,则当
是等差数列,则当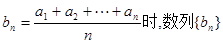 也是等差数列;类比上述性质,相应地
也是等差数列;类比上述性质,相应地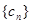 是正项等比数列,当
是正项等比数列,当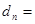 时,数列
时,数列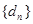 也是等比数列。
也是等比数列。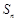 是等差数列{
是等差数列{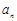 }的前n项和,且
}的前n项和,且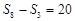 ,则
,则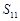 的值为
的值为 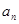 }是等差数列,
}是等差数列,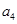 =7,则
=7,则 =_________
=_________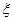 的分布列为,
的分布列为,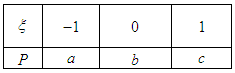
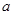 、
、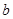 、
、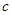 成等差数列,若
成等差数列,若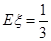 ,则
,则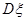 =
=