题目内容
.数列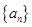 满足:
满足: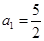 ,且
,且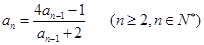
(1)设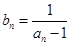 ,证明数列
,证明数列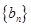 是等差数列;(2)求数列
是等差数列;(2)求数列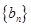 、
、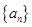 的通项公式;
的通项公式;
(3)设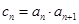 ,
,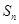 为数列
为数列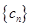 的前
的前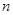 项和,证明
项和,证明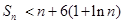 .
.
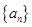 满足:
满足: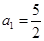 ,且
,且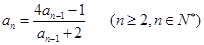
(1)设
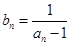 ,证明数列
,证明数列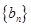 是等差数列;(2)求数列
是等差数列;(2)求数列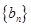 、
、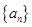 的通项公式;
的通项公式;(3)设
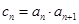 ,
,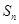 为数列
为数列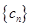 的前
的前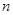 项和,证明
项和,证明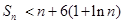 .
.(1) 见解析; (2)
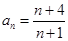 ; (3)证明:见解析。
; (3)证明:见解析。(1) 由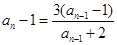 ,
,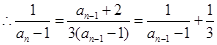
从而证明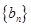 是等差数列.
是等差数列.
(2)在(1)的基础上,可先求出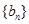 的通项公式,再根据
的通项公式,再根据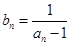 求出
求出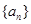 的通项公式.
的通项公式.
(3)先求出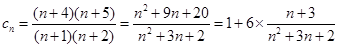
下面解题的关键是确定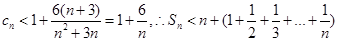 ,
,
然后再考虑数学归纳法进行证明即可.
(1)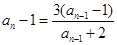 ,
,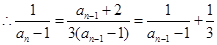
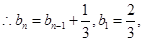
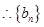 为等差数列
为等差数列
(2)由(1)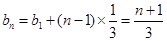 ,从而
,从而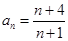
(3)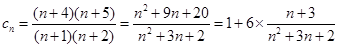
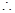
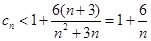 ,
,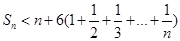 当
当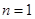 时,
时,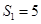 ,不等式的左边=7,不等式成立
,不等式的左边=7,不等式成立
有当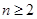 时,
时, 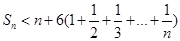
故只要证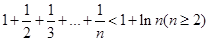 ,
,
如下用数学归纳法给予证明:
①当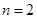 时,
时,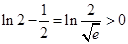 ,
,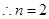 时,不等式成立;
时,不等式成立;
 ②假设当
②假设当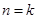 时,
时,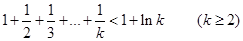 成立
成立
当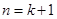 时,
时, 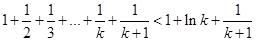
只需证: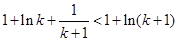 ,即证:
,即证: 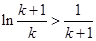
令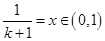 ,则不等式可化为:
,则不等式可化为: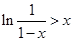
即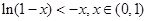
令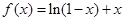 ,则
,则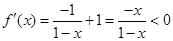
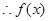 在
在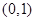 上是减函数
上是减函数
又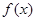 在
在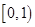 上连续,
上连续, 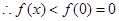 ,故
,故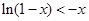
当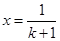 时,有
时,有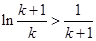
 当
当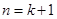 时,所证不等式对
时,所证不等式对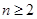 的一切自然数均成立
的一切自然数均成立
综上所述,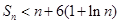 成立.
成立.
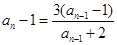 ,
,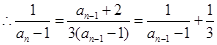
从而证明
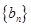 是等差数列.
是等差数列.(2)在(1)的基础上,可先求出
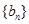 的通项公式,再根据
的通项公式,再根据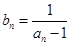 求出
求出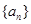 的通项公式.
的通项公式.(3)先求出
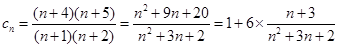
下面解题的关键是确定
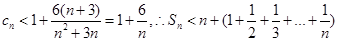 ,
,然后再考虑数学归纳法进行证明即可.
(1)
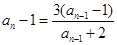 ,
,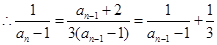
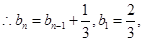
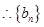 为等差数列
为等差数列 (2)由(1)
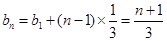 ,从而
,从而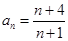
(3)
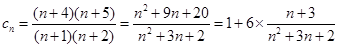
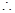
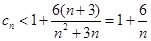 ,
,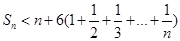 当
当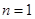 时,
时,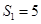 ,不等式的左边=7,不等式成立
,不等式的左边=7,不等式成立有当
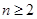 时,
时, 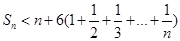
故只要证
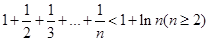 ,
, 如下用数学归纳法给予证明:
①当
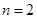 时,
时,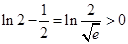 ,
,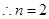 时,不等式成立;
时,不等式成立; ②假设当
②假设当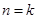 时,
时,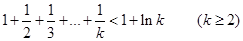 成立
成立当
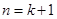 时,
时, 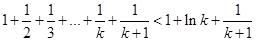
只需证:
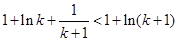 ,即证:
,即证: 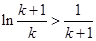
令
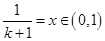 ,则不等式可化为:
,则不等式可化为: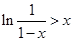
即
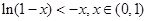
令
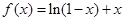 ,则
,则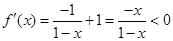
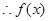 在
在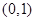 上是减函数
上是减函数又
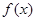 在
在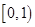 上连续,
上连续, 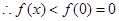 ,故
,故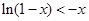
当
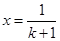 时,有
时,有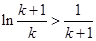
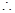 当
当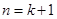 时,所证不等式对
时,所证不等式对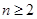 的一切自然数均成立
的一切自然数均成立综上所述,
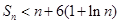 成立.
成立.
练习册系列答案
相关题目
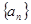 满足
满足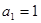 ,
,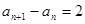 ;数列
;数列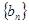 满足
满足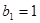 ,
,
 和
和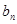 的通项公式
的通项公式 的前
的前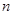 项和
项和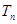
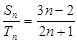 , 则
, 则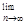
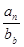 的值是
的值是 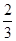
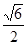
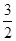
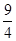
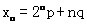 (n∈N+,p、q为常数)且x1,x4,x5成等差数列.
(n∈N+,p、q为常数)且x1,x4,x5成等差数列. 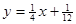 图象上的点, 点列A1(x1,0)、A2(x2,0)、…、An(xn,0)(n∈N) 顺次为x轴正半轴上的点,其中x1=a(0<a<1), 对于任意n∈N,点An、Bn、An+1构成以 Bn为顶点的等腰三角形.
图象上的点, 点列A1(x1,0)、A2(x2,0)、…、An(xn,0)(n∈N) 顺次为x轴正半轴上的点,其中x1=a(0<a<1), 对于任意n∈N,点An、Bn、An+1构成以 Bn为顶点的等腰三角形.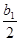 +
+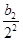 +
+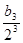 +……+
+……+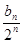 ,(n
,(n N+),
N+), 和等比数列
和等比数列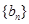 中,
中,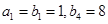 ,
,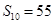 .
.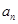 和
和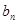 ;
; 为等差数列,
为等差数列,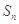 是数列
是数列 ,则
,则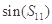 的值为 .
的值为 .