题目内容
【题目】如图,在三棱锥P-ABC中,PA⊥平面ABC,AB⊥AC,PA=AC=3,AB=![]() ,BE=
,BE=![]() EC,AD=2DC.
EC,AD=2DC.

(1)证明:DE⊥平面PAE;
(2)求二面角A-PE-B的余弦值.
【答案】(1)见解析;(2)![]()
【解析】
(1)先证明AB, AC, AP两两垂直,然后以点A为原点建立空间直角坐标系,证明![]() =0,
=0,![]() ,从而得到DE⊥AE,DE⊥AP,故得结论成立.(2)由题意求得平面PEB的法向量
,从而得到DE⊥AE,DE⊥AP,故得结论成立.(2)由题意求得平面PEB的法向量![]() ,又由(1)得
,又由(1)得![]() =(1,-1,0)是平面APE的一个法向量,求出
=(1,-1,0)是平面APE的一个法向量,求出![]() 后再结合图形得到所求的余弦值.
后再结合图形得到所求的余弦值.
(1)证明:
∵PA⊥平面ABC, AB, AC在平面ABC内,
∴PA⊥AB,PA⊥AC.
又AB⊥AC,
∴AB, AC, AP两两垂直,
以点A为坐标原点,AB,AC,AP分别为x,y,z轴建立如图所示的空间直角坐标系,
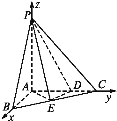
由题意得A(0,0,0),B![]() ,C(0,3,0),P(0,0,3),
,C(0,3,0),P(0,0,3),
∵BE=![]() EC,
EC,
∴E(1,1,0).
∵AD=2DC,
∴D(0,2,0).
∴![]() =(1,-1,0),
=(1,-1,0),![]() =(1,1,0).
=(1,1,0).
∵![]() =0,
=0,
∴![]() ,
,
∴DE⊥AE,
同理可得DE⊥AP,
又AP∩AE=A,
∴DE⊥平面PAE.
(2)解设![]() 是平面PEB的一个法向量,
是平面PEB的一个法向量,
则
令z=1,则![]() ,
,
由(1)得![]() =(1,-1,0)是平面APE的一个法向量,
=(1,-1,0)是平面APE的一个法向量,
∴cos<![]() ,
,![]() >=
>=![]() ,
,
由图形得二面角A-PE-B为锐角,
∴二面角A-PE-B的余弦值为![]() .
.

 名师点睛字词句段篇系列答案
名师点睛字词句段篇系列答案【题目】“中国式过马路”存在很大的交通安全隐患.某调查机构为了解路人对“中国式过马路”的态度是否与性别有关,从马路旁随机抽取30名路人进行了问卷调查,得到了如下列联表:
项目 | 男性 | 女性 | 总计 |
反感 | 10 | ||
不反感 | 8 | ||
总计 | 30 |
已知在这30人中随机抽取1人抽到反感“中国式过马路”的路人的概率是![]() .
.
(1)请将上面的列联表补充完整(直接写结果,不需要写求解过程),并据此资料分析反感“中国式过马路”与性别是否有关?
(2)若从这30人中的女性路人中随机抽取2人参加一活动,记反感“中国式过马路”的人数为X,求X的分布列和数学期望.
附:K2=![]()
.
P(K2≥k0) | 0.10 | 0.05 | 0.010 | 0.005 |
k0 | 2.706 | 3.841 | 6.635 | 7.879 |
