ΧβΡΩΡΎ»ί
ΓΨΧβΡΩΓΩΓΑ÷–Ιζ ΫΙΐ¬μ¬ΖΓ±¥φ‘ΎΚή¥σΒΡΫΜΆ®Α≤»Ϊ“ΰΜΦΘ°Ρ≥Βς≤ιΜζΙΙΈΣΝΥΫβ¬Ζ»ΥΕ‘ΓΑ÷–Ιζ ΫΙΐ¬μ¬ΖΓ±ΒΡΧ§Ε» «Ζώ”κ–‘±π”–ΙΊΘ§¥”¬μ¬Ζ≈‘ΥφΜζ≥ι»Γ30Οϊ¬Ζ»ΥΫχ––ΝΥΈ ΨμΒς≤ιΘ§ΒΟΒΫΝΥ»γœ¬Ν–ΝΣ±μΘΚ
œνΡΩ | Ρ––‘ | ≈°–‘ | ΉήΦΤ |
Ζ¥Η– | 10 | ||
≤ΜΖ¥Η– | 8 | ||
ΉήΦΤ | 30 |
“―÷Σ‘Ύ’β30»Υ÷–ΥφΜζ≥ι»Γ1»Υ≥ιΒΫΖ¥Η–ΓΑ÷–Ιζ ΫΙΐ¬μ¬ΖΓ±ΒΡ¬Ζ»ΥΒΡΗ≈¬ «![]() .
.
(1)«κΫΪ…œΟφΒΡΝ–ΝΣ±μ≤Ι≥δΆξ’ϊ(÷±Ϋ”–¥ΫαΙϊΘ§≤Μ–η“Σ–¥«σΫβΙΐ≥Χ)Θ§≤ΔΨί¥ΥΉ ΝœΖ÷ΈωΖ¥Η–ΓΑ÷–Ιζ ΫΙΐ¬μ¬ΖΓ±”κ–‘±π «Ζώ”–ΙΊΘΩ
(2)»τ¥”’β30»Υ÷–ΒΡ≈°–‘¬Ζ»Υ÷–ΥφΜζ≥ι»Γ2»Υ≤ΈΦ”“ΜΜνΕ·Θ§Φ«Ζ¥Η–ΓΑ÷–Ιζ ΫΙΐ¬μ¬ΖΓ±ΒΡ»Υ ΐΈΣXΘ§«σXΒΡΖ÷≤ΦΝ–ΚΆ ΐ―ßΤΎΆϊΘ°
ΗΫΘΚK2ΘΫ![]()
.
P(K2Γίk0) | 0.10 | 0.05 | 0.010 | 0.005 |
k0 | 2.706 | 3.841 | 6.635 | 7.879 |
ΓΨ¥πΑΗΓΩΘ®1Θ©ΟΜ”–≥δΉψΒΡάμ”…»œΈΣΖ¥Η–ΓΑ÷–Ιζ ΫΙΐ¬μ¬ΖΓ±”κ–‘±π”–ΙΊΘΜ Θ®2Θ©![]() .
.
ΓΨΫβΈωΓΩ
![]() ΗυΨί¥”’β30»Υ÷–ΥφΜζ≥ι»Γ1»Υ≥ιΒΫΖ¥Η–ΓΑ÷–Ιζ ΫΙΐ¬μ¬ΖΓ±ΒΡ¬Ζ»ΥΒΡΗ≈¬ Θ§Ήω≥ωΓΑ÷–Ιζ ΫΙΐ¬μ¬ΖΓ±ΒΡ»Υ ΐΘ§ΫχΕχΒΟ≥ωΡ–…ζΒΡ»Υ ΐΘ§ΧνΚΟ±μΗώΘ§‘ΌΗυΨίΥυΗχΒΡΙΪ Ϋ«σ≥ω
ΗυΨί¥”’β30»Υ÷–ΥφΜζ≥ι»Γ1»Υ≥ιΒΫΖ¥Η–ΓΑ÷–Ιζ ΫΙΐ¬μ¬ΖΓ±ΒΡ¬Ζ»ΥΒΡΗ≈¬ Θ§Ήω≥ωΓΑ÷–Ιζ ΫΙΐ¬μ¬ΖΓ±ΒΡ»Υ ΐΘ§ΫχΕχΒΟ≥ωΡ–…ζΒΡ»Υ ΐΘ§ΧνΚΟ±μΗώΘ§‘ΌΗυΨίΥυΗχΒΡΙΪ Ϋ«σ≥ω![]() ΒΡ÷ΒΘ§»ΜΚσ”κΝΌΫγ÷ΒΉς±»ΫœΘ§Φ¥Ω…ΒΟ≥ωΫα¬έ
ΒΡ÷ΒΘ§»ΜΚσ”κΝΌΫγ÷ΒΉς±»ΫœΘ§Φ¥Ω…ΒΟ≥ωΫα¬έ
![]() XΒΡΩ…Ρή»Γ÷ΒΈΣ0Θ§1Θ§2Θ§Ά®ΙΐΝ–ΨΌΖ®ΒΟΒΫ ¬Φΰ ΐΘ§Ζ÷±πΦΤΥψ≥ωΥϋΟ«ΒΡΗ≈¬ Θ§Ν–≥ωΖ÷≤ΦΝ–Θ§«σ≥ωΤΎΆϊΓΘ
XΒΡΩ…Ρή»Γ÷ΒΈΣ0Θ§1Θ§2Θ§Ά®ΙΐΝ–ΨΌΖ®ΒΟΒΫ ¬Φΰ ΐΘ§Ζ÷±πΦΤΥψ≥ωΥϋΟ«ΒΡΗ≈¬ Θ§Ν–≥ωΖ÷≤ΦΝ–Θ§«σ≥ωΤΎΆϊΓΘ
(1)Ν–ΝΣ±μ≤Ι≥δ»γœ¬ΘΚ
–‘±π | Ρ––‘ | ≈°–‘ | ΉήΦΤ |
Ζ¥Η– | 10 | 6 | 16 |
≤ΜΖ¥Η– | 6 | 8 | 14 |
ΉήΦΤ | 16 | 14 | 30 |
”…“―÷Σ ΐΨίΒΟK2ΒΡΙέ≤β÷ΒK2ΘΫ![]()
Υυ“‘Θ§ΟΜ”–≥δΉψΒΡάμ”…»œΈΣΖ¥Η–ΓΑ÷–Ιζ ΫΙΐ¬μ¬ΖΓ±”κ–‘±π”–ΙΊΘ°
(2)XΒΡΩ…Ρή»Γ÷ΒΈΣ0Θ§1Θ§2.
P(XΘΫ0)ΘΫ![]() Θ§P(XΘΫ1)ΘΫ
Θ§P(XΘΫ1)ΘΫ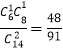 Θ§
Θ§
P(XΘΫ2)ΘΫ![]() Θ§
Θ§
Υυ“‘XΒΡΖ÷≤ΦΝ–ΈΣ
X | 0 | 1 | 2 |
P |
|
|
|
XΒΡ ΐ―ßΤΎΆϊΈΣE(X)ΘΫ![]() .
.

ΓΨΧβΡΩΓΩΚΘΥ°―χ÷≥≥ΓΫχ––Ρ≥Υ°≤ζΤΖΒΡ–¬ΓΔΨ…Άχœδ―χ÷≥ΖΫΖ®ΒΡ≤ζΝΩΕ‘±»Θ§ ’Μώ ±ΗςΥφΜζ≥ι»ΓΝΥ100ΗωΆχœδΘ§≤βΝΩΗςœδΥ°≤ζΤΖΒΡ≤ζΝΩΘ®ΒΞΈΜΘΚkgΘ©, ΤδΤΒ¬ Ζ÷≤Φ÷±ΖΫΆΦ»γœ¬ΘΚ

Θ®1Θ©Φ«A±μ Ψ ¬ΦΰΓΑΨ…―χ÷≥Ζ®ΒΡœδ≤ζΝΩΒΆ”Ύ50 kgΓ±Θ§ΙάΦΤAΒΡΗ≈¬ ΘΜ
Θ®2Θ©Χν–¥œ¬ΟφΝ–ΝΣ±μΘ§≤ΔΗυΨίΝ–ΝΣ±μ≈–Εœ «Ζώ”–99%ΒΡΑ―Έ’»œΈΣœδ≤ζΝΩ”κ―χ÷≥ΖΫΖ®”–ΙΊΘΚ
œδ≤ζΝΩΘΦ50 kg | œδ≤ζΝΩΓί50 kg | |
Ψ…―χ÷≥Ζ® | ||
–¬―χ÷≥Ζ® |
Θ®3Θ©ΗυΨίœδ≤ζΝΩΒΡΤΒ¬ Ζ÷≤Φ÷±ΖΫΆΦΘ§Ε‘’βΝΫ÷÷―χ÷≥ΖΫΖ®ΒΡ”≈Ν”Ϋχ––±»Ϋœ.
ΗΫΘΚ
PΘ® | 0.050 0.010 0.001 |
k | 3.841 6.635 10.828 |
![]() .
. ![]()