题目内容
【题目】在直角坐标系![]() 中,直线
中,直线![]() 的参数方程为
的参数方程为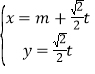 (
(![]() 为参数),以坐标原点
为参数),以坐标原点![]() 为极点,
为极点,![]() 轴正半轴为极轴建立极坐标系,椭圆
轴正半轴为极轴建立极坐标系,椭圆![]() 的极坐标方程为
的极坐标方程为![]() ,其左焦点
,其左焦点![]() 在直线
在直线![]() 上.
上.
(1)若直线![]() 与椭圆
与椭圆![]() 交于
交于![]() 两点,求
两点,求![]() 的值;
的值;
(2)求椭圆![]() 的内接矩形面积的最大值.
的内接矩形面积的最大值.
【答案】(1)![]() ;(2)
;(2)![]() .
.
【解析】
(1)将参数方程化为直角坐标方程可得F的坐标为(![]() ,0),联立直线的参数方程与椭圆方程,结合参数的几何意义计算可得
,0),联立直线的参数方程与椭圆方程,结合参数的几何意义计算可得![]() .
.
(2)结合椭圆方程,设椭圆C上在第一象限内的任意一点M的坐标为(![]() ,4sinθ)(
,4sinθ)(![]() ),据此可得内接矩形关于
),据此可得内接矩形关于![]() 的面积函数,结合三角函数的性质即可确定面积S取得最大值.
的面积函数,结合三角函数的性质即可确定面积S取得最大值.
(1)将![]() 代入ρ2cos2θ+3ρ2sin2θ=48,
代入ρ2cos2θ+3ρ2sin2θ=48,
得x2+3y2=48,即![]() ,
,
因为c2=48-16=32,所以F的坐标为(![]() ,0),
,0),
又因为F在直线l上,所以![]() .
.
把直线l的参数方程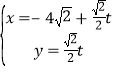 代入x2+3y2=48,
代入x2+3y2=48,
化简得t2-4t-8=0,所以t1+t2=4,t1t2=-8,
所以![]() .
.
(2)由椭圆C的方程![]() ,可设椭圆C上在第一象限内的任意一点M的坐标为(
,可设椭圆C上在第一象限内的任意一点M的坐标为(![]() ,4sinθ)(
,4sinθ)(![]() ),
),
所以内接矩形的面积![]() ,
,
当![]() 时,面积S取得最大值
时,面积S取得最大值![]() .
.

练习册系列答案
相关题目