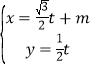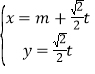ΧβΡΩΡΎ»ί
ΓΨΧβΡΩΓΩΡ≥ΒΊ«χΙΛΜαάϊ”ΟΓΑΫΓ≤Ϋ––![]() Γ±ΩΣ’ΙΟςΡξΫΓ≤ΫΉΏΜΐΖ÷Ϋ±άχΜνΕ·.Μα‘±ΟΩΧλΉΏ5«ß≤ΫΩ…ΜώΜΐΖ÷30Ζ÷(≤ΜΉψ5«ß≤Ϋ≤ΜΜΐΖ÷)Θ§ΟΩΕύΉΏ2«ß≤Ϋ‘ΌΜΐ20Ζ÷(≤ΜΉψ2«ß≤Ϋ≤ΜΜΐΖ÷).ΈΣΝΥΫβΜα‘±ΒΡΫΓ≤ΫΉΏ«ιΩωΘ§ΙΛΜα‘ΎΡ≥Χλ¥”œΒΆ≥÷–ΥφΜζ≥ι»ΓΝΥ1000ΟϊΜα‘±Θ§Ά≥ΦΤΝΥΒ±ΧλΥϊΟ«ΒΡ≤Ϋ ΐΘ§≤ΔΫΪ―υ±Ψ ΐΨίΖ÷ΈΣ
Γ±ΩΣ’ΙΟςΡξΫΓ≤ΫΉΏΜΐΖ÷Ϋ±άχΜνΕ·.Μα‘±ΟΩΧλΉΏ5«ß≤ΫΩ…ΜώΜΐΖ÷30Ζ÷(≤ΜΉψ5«ß≤Ϋ≤ΜΜΐΖ÷)Θ§ΟΩΕύΉΏ2«ß≤Ϋ‘ΌΜΐ20Ζ÷(≤ΜΉψ2«ß≤Ϋ≤ΜΜΐΖ÷).ΈΣΝΥΫβΜα‘±ΒΡΫΓ≤ΫΉΏ«ιΩωΘ§ΙΛΜα‘ΎΡ≥Χλ¥”œΒΆ≥÷–ΥφΜζ≥ι»ΓΝΥ1000ΟϊΜα‘±Θ§Ά≥ΦΤΝΥΒ±ΧλΥϊΟ«ΒΡ≤Ϋ ΐΘ§≤ΔΫΪ―υ±Ψ ΐΨίΖ÷ΈΣ![]() Θ§
Θ§![]() Θ§
Θ§![]() Θ§
Θ§![]() Θ§
Θ§![]() Θ§
Θ§![]() Θ§
Θ§![]() Θ§
Θ§![]() Θ§
Θ§![]() Ψ≈ΉιΘ§’ϊάμΒΟΒΫ»γœ¬ΤΒ¬ Ζ÷≤Φ÷±ΖΫΆΦΘΚ
Ψ≈ΉιΘ§’ϊάμΒΟΒΫ»γœ¬ΤΒ¬ Ζ÷≤Φ÷±ΖΫΆΦΘΚ
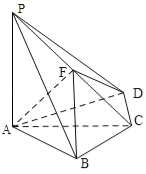
Θ®1Θ©¥”Β±Χλ≤Ϋ ΐ‘Ύ![]() Θ§
Θ§![]() Θ§
Θ§![]() ΒΡΜα‘±÷–Α¥Ζ÷≤ψ≥ι―υΒΡΖΫ Ϋ≥ι»Γ6»ΥΘ§‘Ό¥”’β6»Υ÷–ΥφΜζ≥ι»Γ2»ΥΘ§«σ’β2»ΥΜΐΖ÷÷°ΚΆ≤Μ…Ό”Ύ220Ζ÷ΒΡΗ≈¬ ΘΜ
ΒΡΜα‘±÷–Α¥Ζ÷≤ψ≥ι―υΒΡΖΫ Ϋ≥ι»Γ6»ΥΘ§‘Ό¥”’β6»Υ÷–ΥφΜζ≥ι»Γ2»ΥΘ§«σ’β2»ΥΜΐΖ÷÷°ΚΆ≤Μ…Ό”Ύ220Ζ÷ΒΡΗ≈¬ ΘΜ
Θ®2Θ©«σΗΟΉι ΐΨίΒΡ÷–ΈΜ ΐ.
ΓΨ¥πΑΗΓΩΘ®1Θ©![]() ΘΜΘ®2Θ©
ΘΜΘ®2Θ©![]() .
.
ΓΨΫβΈωΓΩ
Θ®1Θ©ΗυΨίΖ÷≤ψ≥ι―υΒΡ±»άΐ ΫΩ…÷ΣΘ§![]() Θ§
Θ§![]() Θ§
Θ§![]() ΒΡΜα‘±÷–Θ§Ζ÷±π≥ι»Γ3»ΥΘ§2»ΥΘ§1»ΥΘ§ΦΤΥψœύ”ΠΜΐΖ÷ΈΣ90Ζ÷Θ§110Ζ÷Θ§130Ζ÷Θ§‘ρΩ…“άΨίΧβ“β«σ≥ωΗ≈¬ ΘΜ
ΒΡΜα‘±÷–Θ§Ζ÷±π≥ι»Γ3»ΥΘ§2»ΥΘ§1»ΥΘ§ΦΤΥψœύ”ΠΜΐΖ÷ΈΣ90Ζ÷Θ§110Ζ÷Θ§130Ζ÷Θ§‘ρΩ…“άΨίΧβ“β«σ≥ωΗ≈¬ ΘΜ
Θ®2Θ©’“≥ωΗ≈¬ ΈΣ0.5 ±Θ§Ε‘”ΠΒΡ≤Ϋ ΐΦ¥Ω…Θ§≤Ϋ ΐΈΣ![]() ±Ε‘”ΠΒΡΗ≈¬ ΈΣΘΚ
±Ε‘”ΠΒΡΗ≈¬ ΈΣΘΚ![]() Θ§Ι Η≈¬ ΈΣ0.5 ±Ε‘”Π≤Ϋ ΐΘ§Ω…Α¥±»άΐ«σΘ§ΈΣ
Θ§Ι Η≈¬ ΈΣ0.5 ±Ε‘”Π≤Ϋ ΐΘ§Ω…Α¥±»άΐ«σΘ§ΈΣ![]()
Θ®1Θ©Α¥Ζ÷≤ψ≥ι―υΒΡΖΫΖ®Θ§‘Ύ![]() ”Π≥ι»Γ3»ΥΘ§
”Π≥ι»Γ3»ΥΘ§
Φ«ΈΣ![]() Θ§
Θ§![]() Θ§
Θ§![]() Θ§ΟΩ»ΥΒΡΜΐΖ÷ «90Ζ÷ΘΜ
Θ§ΟΩ»ΥΒΡΜΐΖ÷ «90Ζ÷ΘΜ
‘Ύ![]() ΡΎ”Π≥ι»Γ2»ΥΘ§Φ«ΈΣ
ΡΎ”Π≥ι»Γ2»ΥΘ§Φ«ΈΣ![]() Θ§
Θ§![]() Θ§ΟΩ»ΥΒΡΜΐΖ÷ «110Ζ÷ΘΜ
Θ§ΟΩ»ΥΒΡΜΐΖ÷ «110Ζ÷ΘΜ
‘Ύ![]() ”Π≥ι»Γ1»ΥΘ§Φ«ΈΣcΘ§ΟΩ»ΥΒΡΜΐΖ÷ «130 Ζ÷ΘΜ
”Π≥ι»Γ1»ΥΘ§Φ«ΈΣcΘ§ΟΩ»ΥΒΡΜΐΖ÷ «130 Ζ÷ΘΜ
¥”6»Υ÷–ΥφΜζ≥ι»Γ2»ΥΘ§”–![]() Θ§
Θ§![]() Θ§
Θ§![]() Θ§
Θ§![]() Θ§
Θ§![]() Θ§
Θ§![]() Θ§
Θ§
![]() Θ§
Θ§![]() Θ§
Θ§![]() Θ§
Θ§![]() Θ§
Θ§![]() Θ§
Θ§![]() Θ§
Θ§![]() Θ§
Θ§![]() Θ§
Θ§![]() Ι≤15÷÷ΖΫΖ®.
Ι≤15÷÷ΖΫΖ®.
Υυ“‘¥”6»Υ÷–ΥφΜζ≥ι»Γ2»ΥΘ§’β2»ΥΒΡΜΐΖ÷÷°ΚΆ≤Μ…Ό”Ύ220Ζ÷ΒΡ”–![]() Θ§
Θ§
![]() Θ§
Θ§![]() Θ§
Θ§![]() Θ§
Θ§![]() Θ§
Θ§![]() Ι≤ 6 ÷÷ΖΫΖ®.
Ι≤ 6 ÷÷ΖΫΖ®.
…η¥”6»Υ÷–ΥφΜζ≥ι»Γ2»ΥΘ§’β2»ΥΒΡΜΐΖ÷÷°ΚΆ≤Μ…Ό”Ύ220Ζ÷ΈΣ ¬ΦΰAΘ§
‘ρ![]() .
.
Θ®2Θ©ΓΏΒ±≤Ϋ ΐΈΣ![]() ±Ε‘”ΠΒΡ»Υ ΐΥυ’Φ±»άΐΈΣΘΚ
±Ε‘”ΠΒΡ»Υ ΐΥυ’Φ±»άΐΈΣΘΚ![]()
Γύ÷Μ–η’“≥ω![]() ÷–»Υ ΐ’Φ0.2 ±ΥυΕ‘”ΠΒΡ≤Ϋ ΐΦ¥Ω…
÷–»Υ ΐ’Φ0.2 ±ΥυΕ‘”ΠΒΡ≤Ϋ ΐΦ¥Ω…
ΓύΤδ≤Ϋ ΐΈΣΘΚ11+![]() ΈΣΤδ÷–ΈΜ ΐ.
ΈΣΤδ÷–ΈΜ ΐ.

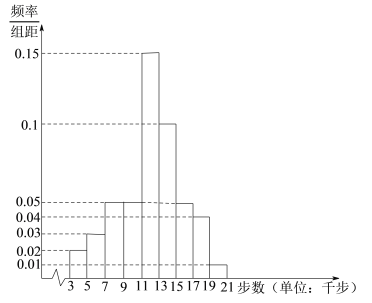
 άηΟςΈΡΜ·Κ°ΦΌΉς“ΒœΒΝ–¥πΑΗ
άηΟςΈΡΜ·Κ°ΦΌΉς“ΒœΒΝ–¥πΑΗ Κ°ΦΌΧλΒΊ÷Ί«λ≥ωΑφ…γœΒΝ–¥πΑΗ
Κ°ΦΌΧλΒΊ÷Ί«λ≥ωΑφ…γœΒΝ–¥πΑΗ