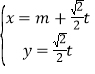Question

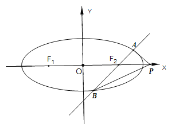
【题目】如图,椭圆：的左、右焦点分别为,椭圆上一点与两焦点构成的三角形的周长为,离心率为.

（Ⅰ）求椭圆的方程；

（Ⅱ）过点的直线交椭圆于两点,问在轴上是否存在定点,使得为定值？证明你的结论.

Answer 1

【答案】（1）（2）

【解析】

（Ⅰ）利用椭圆的定义和离心率公式、以及a，b，c的关系，求出a的值，进而可求b的值，即可得到椭圆的标准方程；

（Ⅱ）当直线的斜率存在时,设此时直线的方程为代入椭圆的方程,消去并整理得，利用韦达定理表示，从而得到定点，检验直线l的斜率不存在时也适合题意.

,．

（Ⅰ）由题设得2a+2c=6,又e==,解得a=2，c=1,∴b=.

故椭圆的方程为.

（Ⅱ）右焦点为（1，0），当直线的斜率存在时,设此时直线的方程为,

设A（x1，y1），B（x2，y2）,把,代入椭圆的方程,消去并整理得,

,则,

可得.设点,

那么 ,

,

若轴上存在定点,使得为定值,则有,解得,

此时,

当直线l的斜率不存在时,此时直线l的方程为x=1,把x=1代入椭圆方程解得,

此时,,

综上,在轴上存在定点,使得为定值.