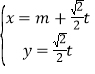题目内容
【题目】已知函数y＝a－bcos
(b＞0)的最大值为
，最小值为-
.
(1)求a，b的值；
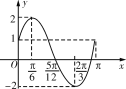
(2)求函数g(x)＝－4asin
的最小值并求出对应x的集合.
【答案】(1)a=
,b=1；(2)
.
【解析】
(1) 由函数y＝a－bcos
(b＞0)的最大值为
，最小值为-，可列关于a、b的方程组，解之可得a，b的值；
(2)可得 g(x)＝－2sin(
)，利用三角函数的性质可得其最小值与对应x的集合.
解：(1)易得cos(
)∈[－1，1]，∵b＞0，∴－b＜0.
∴
∴a＝
，b＝1.
(2)由(1)知g(x)＝－2sin()，∵sin()∈[－1，1]，∴g(x)∈[－2，2].
∴g(x)的最小值为－2，此时，sin()＝1.
对应x的集合为
.
练习册系列答案
百年学典课时学练测系列答案
相关题目
【题目】某快递公司收取快递费用的标准是：重量不超过
的包裹收费10元；重量超过的包裹，除收费10元之外，超过的部分，每超出（不足时按计算）需再收5元.公司从承揽过的包裹中，随机抽取100件，其重量统计如下：
包裹重量（单位： |
|
|
|
|
|
包裹件数 | 43 | 30 | 15 | 8 | 4 |
公司又随机抽取了60天的揽件数，得到频数分布表如下：
揽件数 |
|
|
|
|
|
天数 | 6 | 6 | 30 | 12 | 6 |
以记录的60天的揽件数的频率作为各揽件数发生的概率
（1）计算该公司3天中恰有2天揽件数在
的概率；
（2）估计该公司对每件包裹收取的快递费的平均值；
（3）公司将快递费的三分之一作为前台工作人员的工资和公司利润，剩余的用做其他费用，目前前台有工作人员3人，每人每天揽件不超过150件，每人每天工资100元，公司正在考虑是否将前台工作人员裁减1人，试计算裁员前后公司每日利润的数学期望，并判断裁员是否对提高公司利润有利？
（注：同一组中的揽件数以这组数据所在区间中点值作代表）
