题目内容
【题目】已知圆C经过点![]() ,
,![]() ,且圆心在直线
,且圆心在直线![]() 上
上
(1)求圆C的方程.
(2)过点![]() 的直线与圆C交于A,B两点,问:在直线
的直线与圆C交于A,B两点,问:在直线![]() 上是否存在定点N,使得
上是否存在定点N,使得![]() (
(![]() ,
,![]() 分别为直线AN,BN的斜率)恒成立?若存在,请求出点N的坐标;若不存在,请说明理由.
分别为直线AN,BN的斜率)恒成立?若存在,请求出点N的坐标;若不存在,请说明理由.
【答案】(1)![]() ;(2)存在定点
;(2)存在定点![]() ,使得
,使得![]() 恒成立
恒成立
【解析】
(1)![]() 的垂直平分线与直线
的垂直平分线与直线![]() 的交点就是圆心,求出圆心即可得到半径,圆的方程得解;
的交点就是圆心,求出圆心即可得到半径,圆的方程得解;
(2)设直线AB的方程为![]() ,联立直线与圆的方程,消去y整理得
,联立直线与圆的方程,消去y整理得![]() ,根据
,根据![]() 建立等式,结合韦达定理求出定点,检验直线斜率为0和斜率不存在的情况.
建立等式,结合韦达定理求出定点,检验直线斜率为0和斜率不存在的情况.
(1)由题可知线段EF的中点为![]() ,EF的垂直平分线的斜率为5,
,EF的垂直平分线的斜率为5,
![]() 的垂直平分线的方程为
的垂直平分线的方程为![]() .
.
EF的垂直平分线与直线l的交点即为圆心C,
由![]() ,解得
,解得![]() ,即
,即![]() .
.
又![]() ,
,
![]() 圆C的方程为
圆C的方程为![]() .
.
(2)当直线AB的斜率存在且不为0时,设直线AB的斜率为k,则过点![]() 的直线AB的方程为
的直线AB的方程为![]() ,由
,由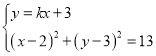 ,消去y整理得
,消去y整理得![]() .
.
设![]() ,
,![]() ,
,
![]() ,
,![]() .(*)
.(*)
设![]() ,则
,则![]() ,
,![]() .
.
![]() ,
,
![]() ,
,![]() ,
,
即![]() ,
,
将(*)式代入得![]() ,
,
解得![]() 故点N的坐标为
故点N的坐标为![]() .
.
当直线AB的斜率为0时,显然点![]() 可使
可使![]() 成立.
成立.
当直线AB的斜率不存在时,直线AB的方程为![]() ,
,![]() ,
,![]() ,显然点N可使
,显然点N可使![]() 成立.
成立.
![]() 在直线
在直线![]() 上存在定点
上存在定点![]() 使得
使得![]() 恒成立.
恒成立.

练习册系列答案
 阳光考场单元测试卷系列答案
阳光考场单元测试卷系列答案 名校联盟冲刺卷系列答案
名校联盟冲刺卷系列答案 名校提分一卷通系列答案
名校提分一卷通系列答案 课程达标测试卷闯关100分系列答案
课程达标测试卷闯关100分系列答案
相关题目