题目内容
(本小题满分16分)
设数列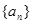 的前项和为
的前项和为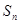 ,已知
,已知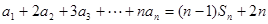 (
( ).
).
(1)求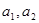 的值;
的值;
(2)求证:数列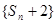 是等比数列;
是等比数列;
(3)抽去数列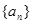 中的第1项,第4项,第7项,……,第
中的第1项,第4项,第7项,……,第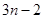 项,……,余下的项顺序不变,组成一个新数列
项,……,余下的项顺序不变,组成一个新数列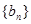 ,若
,若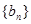 的前
的前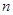 项的和为
项的和为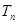 ,求证:
,求证: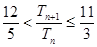 .
.
设数列
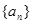 的前项和为
的前项和为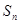 ,已知
,已知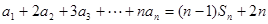 (
(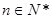 ).
).(1)求
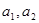 的值;
的值;(2)求证:数列
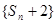 是等比数列;
是等比数列;(3)抽去数列
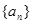 中的第1项,第4项,第7项,……,第
中的第1项,第4项,第7项,……,第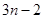 项,……,余下的项顺序不变,组成一个新数列
项,……,余下的项顺序不变,组成一个新数列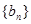 ,若
,若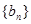 的前
的前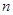 项的和为
项的和为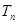 ,求证:
,求证: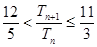 .
.(1)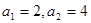
(2)见解析
(3)见解析
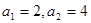
(2)见解析
(3)见解析
(1)令n=1和n=2求出数列的前2项;(2)利用已知式子构造递推式子,作差得出关于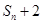 的递推式,然后根据等比数列的概念求出数列
的递推式,然后根据等比数列的概念求出数列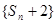 的通项;(3)先根据数列的前N项和知识求出
的通项;(3)先根据数列的前N项和知识求出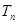 ,然后利用放缩思想求出
,然后利用放缩思想求出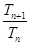 的范围
的范围
解:(1)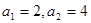
(2)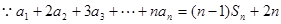 ,①
,①
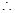 当
当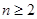 时,
时,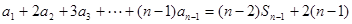 。②
。②
由①-②,得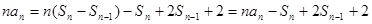
所以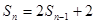 ,
,
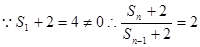
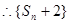 是以4为首项,2为公比的等比数列。
是以4为首项,2为公比的等比数列。
(3)由(2)得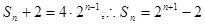 ,
,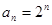
抽去数列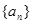 中得第1项、第4项、第7项、…、第
中得第1项、第4项、第7项、…、第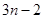 项得到数列为
项得到数列为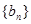 为
为
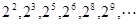 ,
, 它的奇数项组成一个以4为首项,8为公比的等比数列,偶数项组成一个以8为首项,8为公比的等比数列。
它的奇数项组成一个以4为首项,8为公比的等比数列,偶数项组成一个以8为首项,8为公比的等比数列。
所以当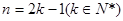 时
时
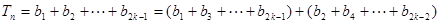
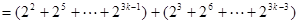
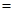
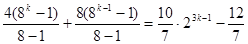
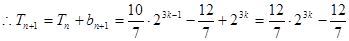
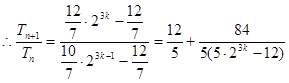
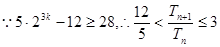 。
。
当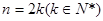 时
时
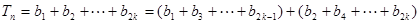
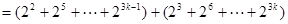
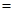
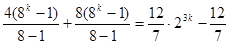
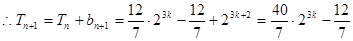
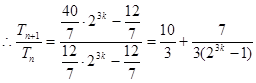
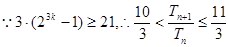 。
。
综上,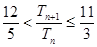
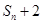 的递推式,然后根据等比数列的概念求出数列
的递推式,然后根据等比数列的概念求出数列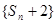 的通项;(3)先根据数列的前N项和知识求出
的通项;(3)先根据数列的前N项和知识求出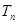 ,然后利用放缩思想求出
,然后利用放缩思想求出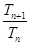 的范围
的范围解:(1)
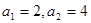
(2)
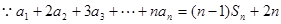 ,①
,①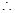 当
当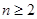 时,
时,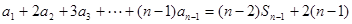 。②
。②由①-②,得
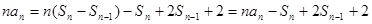
所以
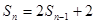 ,
,
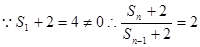
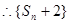 是以4为首项,2为公比的等比数列。
是以4为首项,2为公比的等比数列。(3)由(2)得
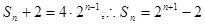 ,
,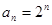
抽去数列
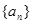 中得第1项、第4项、第7项、…、第
中得第1项、第4项、第7项、…、第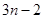 项得到数列为
项得到数列为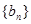 为
为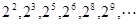 ,
,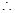 它的奇数项组成一个以4为首项,8为公比的等比数列,偶数项组成一个以8为首项,8为公比的等比数列。
它的奇数项组成一个以4为首项,8为公比的等比数列,偶数项组成一个以8为首项,8为公比的等比数列。所以当
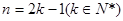 时
时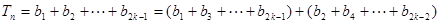
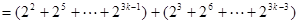
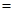
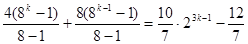
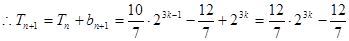
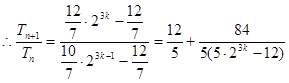
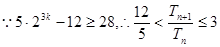 。
。当
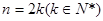 时
时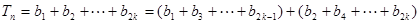
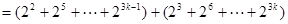
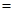
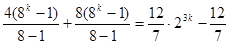
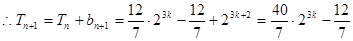
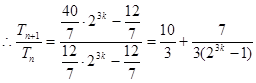
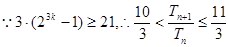 。
。综上,

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
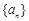 和
和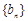 满足:
满足: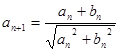 ,
,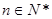 ,
,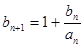 ,
,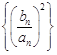 是等差数列;
是等差数列;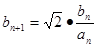 ,
,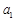 和
和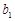 的值.
的值.
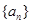 为等差数列,
为等差数列,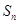 为其前n项和,若
为其前n项和,若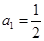 ,
,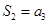 ,则
,则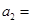 ,
,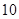 项的和为
项的和为 项的和为
项的和为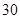 ,则前
,则前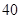 项的和为 ▲ .
项的和为 ▲ .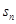 为前n个圆的面积之和,则
为前n个圆的面积之和,则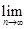
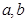 ,可按规则
,可按规则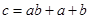 扩充为一个新数
扩充为一个新数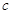 ,在
,在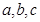 三个数中取两个较大的数,按上述规则扩充得到一个新数,依次下去,将每扩充一次得到一个新数称为一次操作.若
三个数中取两个较大的数,按上述规则扩充得到一个新数,依次下去,将每扩充一次得到一个新数称为一次操作.若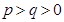 ,经过6次操作后扩充所得的数为
,经过6次操作后扩充所得的数为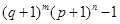 (
(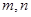 为正整数),则
为正整数),则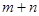 的值为 ▲ .
的值为 ▲ .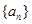 是首项为0的递增数列,
是首项为0的递增数列,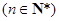 ,
,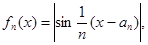
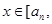
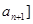 满足:对于任意的
满足:对于任意的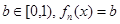 总有两个不同的根. (Ⅰ)试写出
总有两个不同的根. (Ⅰ)试写出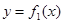 ,并求出
,并求出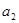 ;
; 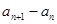 ,并求出
,并求出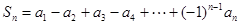 ,求
,求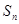 .
.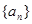 中,
中,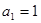 ,
, ,数列
,数列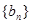 中,
中,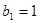 ,且点
,且点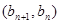 在直线
在直线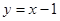 上。
上。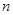 项和
项和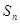 ;
;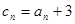 ,求数列
,求数列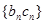 的前
的前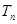 ;
;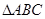 的三内角
的三内角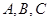 成等差数列,且
成等差数列,且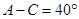 ,则
,则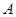 = .
= .