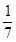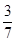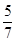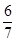题目内容
已知各项均为正数的两个数列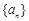 和
和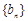 满足:
满足: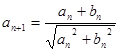 ,
,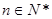 ,
,
(1)设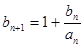 ,
,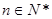 ,求证:数列
,求证:数列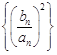 是等差数列;
是等差数列;
(2)设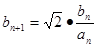 ,
,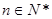 ,且
,且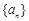 是等比数列,求
是等比数列,求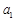 和
和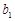 的值.
的值.
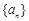 和
和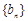 满足:
满足: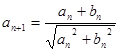 ,
,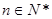 ,
,(1)设
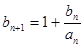 ,
,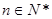 ,求证:数列
,求证:数列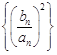 是等差数列;
是等差数列;(2)设
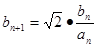 ,
,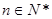 ,且
,且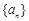 是等比数列,求
是等比数列,求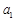 和
和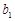 的值.
的值.
(1)见解析
(2)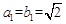
(2)
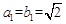
(1)根据题设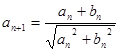 和
和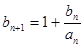 ,求出
,求出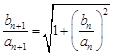 ,从而证明
,从而证明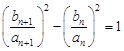 而得证。
而得证。
(2)根据基本不等式得到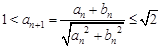 ,用反证法证明等比数列
,用反证法证明等比数列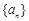 的公比
的公比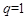 。
。
从而得到 的结论,再由
的结论,再由 知
知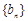 是公比是
是公比是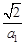 的等比数列。最后用反证法求出
的等比数列。最后用反证法求出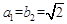
解:(1)∵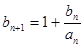 ,∴
,∴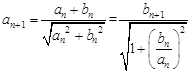 。
。
∴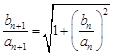 。
。
∴ 。
。
∴数列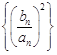 是以1 为公差的等差数列。
是以1 为公差的等差数列。
(2)∵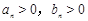 ,∴
,∴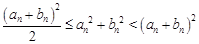 。
。
∴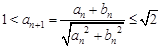 。(﹡)
。(﹡)
设等比数列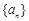 的公比为
的公比为 ,由
,由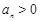 知
知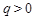 ,下面用反证法证明
,下面用反证法证明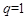
若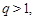 则
则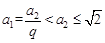 ,∴当
,∴当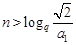 时,
时,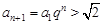 ,与(﹡)矛盾。
,与(﹡)矛盾。
若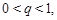 则
则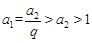 ,∴当
,∴当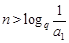 时,
时,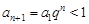 ,与(﹡)矛盾。
,与(﹡)矛盾。
∴综上所述,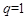 。∴
。∴ ,∴
,∴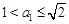 。
。
又∵
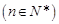 ,∴
,∴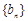 是公比是
是公比是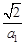 的等比数列。
的等比数列。
若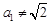 ,则
,则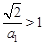 ,于是
,于是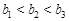 。
。
又由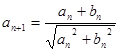 即
即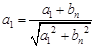 ,得
,得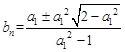 。
。
∴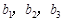 中至少有两项相同,与
中至少有两项相同,与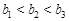 矛盾。∴
矛盾。∴ 。
。
∴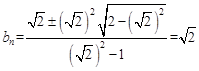 。
。
∴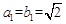
【考点定位】本题综合考查等差数列的定义、等比数列的有关知识的灵活运用,指数幂和根式的互化,数列通项公式的求解,注意利用等差数列的定义证明问题时一般思路和基本方法,本题是有关数列的综合题,从近几年的高考命题趋势看,数列问题仍是高考的热点、重点问题,在训练时,要引起足够的重视。
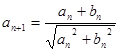 和
和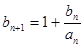 ,求出
,求出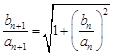 ,从而证明
,从而证明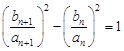 而得证。
而得证。(2)根据基本不等式得到
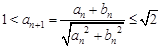 ,用反证法证明等比数列
,用反证法证明等比数列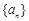 的公比
的公比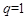 。
。从而得到
 的结论,再由
的结论,再由 知
知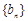 是公比是
是公比是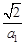 的等比数列。最后用反证法求出
的等比数列。最后用反证法求出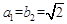
解:(1)∵
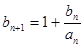 ,∴
,∴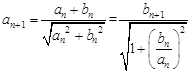 。
。∴
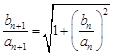 。
。∴
 。
。∴数列
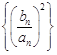 是以1 为公差的等差数列。
是以1 为公差的等差数列。(2)∵
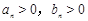 ,∴
,∴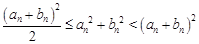 。
。∴
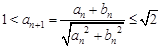 。(﹡)
。(﹡)设等比数列
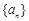 的公比为
的公比为 ,由
,由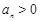 知
知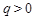 ,下面用反证法证明
,下面用反证法证明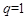
若
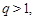 则
则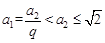 ,∴当
,∴当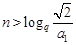 时,
时,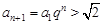 ,与(﹡)矛盾。
,与(﹡)矛盾。若
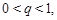 则
则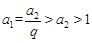 ,∴当
,∴当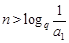 时,
时,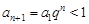 ,与(﹡)矛盾。
,与(﹡)矛盾。∴综上所述,
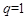 。∴
。∴ ,∴
,∴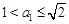 。
。又∵

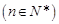 ,∴
,∴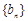 是公比是
是公比是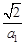 的等比数列。
的等比数列。若
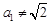 ,则
,则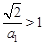 ,于是
,于是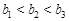 。
。又由
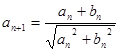 即
即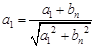 ,得
,得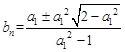 。
。∴
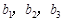 中至少有两项相同,与
中至少有两项相同,与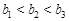 矛盾。∴
矛盾。∴ 。
。∴
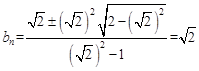 。
。∴
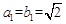
【考点定位】本题综合考查等差数列的定义、等比数列的有关知识的灵活运用,指数幂和根式的互化,数列通项公式的求解,注意利用等差数列的定义证明问题时一般思路和基本方法,本题是有关数列的综合题,从近几年的高考命题趋势看,数列问题仍是高考的热点、重点问题,在训练时,要引起足够的重视。

练习册系列答案
 考前必练系列答案
考前必练系列答案
相关题目
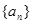 的前项和为
的前项和为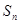 ,已知
,已知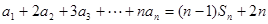 (
(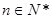 ).
).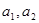 的值;
的值;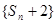 是等比数列;
是等比数列;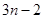 项,……,余下的项顺序不变,组成一个新数列
项,……,余下的项顺序不变,组成一个新数列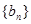 ,若
,若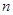 项的和为
项的和为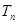 ,求证:
,求证: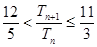 .
.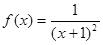 ,数列
,数列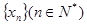 的项满足:
的项满足: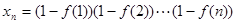 ,(1)试求
,(1)试求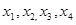
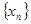 的通项,并利用数学归纳法证明.
的通项,并利用数学归纳法证明.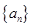 的前
的前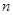 项和
项和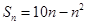 ,
,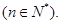
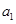 和
和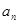 ;
; 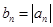 ,求数列
,求数列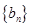 的前
的前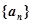 中,
中,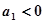 ,又
,又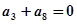 ,则使数列
,则使数列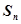 取最小值时的n的值是 。
取最小值时的n的值是 。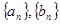 满足:
满足: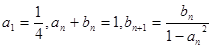
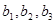 的值; 2)求证数列
的值; 2)求证数列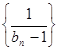 是等差数列,并求数列
是等差数列,并求数列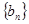 的通项公式;
的通项公式;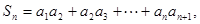 若
若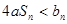 恒成立,求实数
恒成立,求实数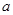 的取值范围.
的取值范围.
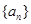 为等差数列,且
为等差数列,且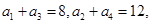 (Ⅰ)求数列
(Ⅰ)求数列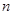 项和为
项和为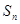 ,若
,若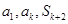 成等比数列,求正整数
成等比数列,求正整数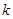 的值。
的值。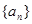 满足
满足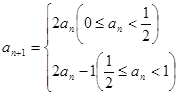 若
若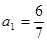 ,则
,则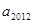 的值为:( )
的值为:( )