题目内容

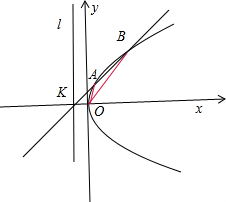
设抛物线y2=2px（p为常数）的准线与X轴交于点K，过K的直线l与抛物线交于A、B两点，则
OA
•
OB
=______．
如图所示，
设点A（x1，y1），B（x2，y2）．
设直线l：my=x+
p
2
．
联立
my=x+
p
2
y2=2px
化为y2-2pmy+p2=0．
∵直线l与抛物线相交于不同两点，∴△＞0，化为m2＞1．
∴y1+y2=2pm，y1y2=p2．
∴
OA
•
OB
=x1x2+y1y2=(my1-
p
2
)(my2-
p
2
)+y1y2
=（m2+1）y1y2-
pm
2
(y1+y2)+
p2
4

=(m2+1)•p2-
pm
2
•2pm+
p2
4

=
5
4
p2．
故答案为
5
4
p2．
练习册系列答案
相关题目
(本小题满分12分)

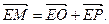如图，在矩形ABCD中，已知A（2，0）、C（－2，2），点P在BC边上移动，线段OP的垂直平分线交y轴于点E，点M满足(Ⅰ)求点M的轨迹方程；
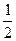(Ⅱ)已知点F（0，），过点F的直线l与点M的轨迹相交于Q、R两点，且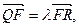求实数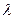的取值范围.
长方形ABCD，AB=2
2
，BC=1，以AB的中点O为原点建立如图所示的平面直角坐标系．
（1）求以A、B为焦点，且过C、D两点的椭圆的标准方程：
（2）过点p（0，2）的直线m与（1）中椭圆只有一个公共点，求直线m的方程：
（3）过点p（0，2）的直线l交（1）中椭圆与M，N两点，是否存在直线l，使得以弦MN为直径的圆恰好过原点？若存在，直线l的方程；若不存在，说明理由．
若点（3，1）是抛物线y2=2px（p＞0）的一条弦的中点，且这条弦所在直线的斜率为2，则p=______．
抛物线的顶点在原点O，焦点为椭圆
x2
3
+
y2
2
=1的右焦点F．
（1）求抛物线的方程；
（2）设点P在抛物线上运动，求P到直线y=x+3的距离的最小值，并求此时点P的坐标．
已知双曲线C的渐近线为y=±
3
x且过点M（1，
2
）．
（1）求双曲线C的方程；
（2）若直线y=ax+1与双曲线C相交于A，B两点，O为坐标原点，若OA与OB垂直，求a的值．
如图，从椭圆E：
x2
a2
+
y2
b2
=1(a＞b＞0)上一点P向x轴作垂线，垂足恰为左焦点F1，又点A是椭圆与x轴正半轴的交点，点B是椭圆与y轴正半轴的交点，且AB∥OP，|F1A|=
10
+
5
，
（1）求椭圆E的方程．
（2）是否存在圆心在原点的圆，使得该圆的任意一条切线与椭圆E恒有两个交点C，D，且
OC
⊥
OD
？若存在，写出该圆的方程，并求|CD|的取值范围；若不存在，说明理由．
已知椭圆E：
x2
a2
+y2=1（a＞1）的离心率e=
3
2
，直线x=2t（t＞0）与椭圆E交于不同的两点M、N，以线段MN为直径作圆C，圆心为C
（Ⅰ）求椭圆E的方程；
（Ⅱ）当圆C与y轴相切的时候，求t的值；
（Ⅲ）若O为坐标原点，求△OMN面积的最大值．
F1，F2是双曲线
x2
a2
-
y2
b2
=1(a＞0，b＞0)的左右焦点，Q是双曲线上动点，从左焦点引∠F1QF2的平分线的垂线，垂足为P，则P点的轨迹是（　　）的一部分．
A．圆B．椭圆C．双曲线D．抛物线

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网