题目内容
已知椭圆
+y2=1,其右焦点为F,直线l经过点F与椭圆交于A,B两点,且|AB|=
.
(1)求直线l的方程;
(2)求△OAB的面积.
| x2 |
| 2 |
4
| ||
| 3 |
(1)求直线l的方程;
(2)求△OAB的面积.
(1)∵椭圆的标准方程为:
+y2=1
故c=1
则其右焦点的坐标为F(1,0)
当斜率不存在时,直线l的方程为x=1
此时|AB|=
=
,不符合条件;
当斜率存在时,设直线l的方程为y=k(x-1),A(x1,y1),B(x2,y2),
则有
得:(1+2k2)x2-4k2x+2k2-2=0
则x1+x2=
,x1x2=
∴|AB|=
•
=
×
=
解得k=±1
故直线l的方程为:x+y-1=0或x-y-1=0
(2)原点到直线x+y-1=0或x-y-1=0的距离d=
=
故△OAB的面积S=
×
×
=
| x2 |
| 2 |
故c=1
则其右焦点的坐标为F(1,0)
当斜率不存在时,直线l的方程为x=1
此时|AB|=
| 2b2 |
| a |
| 2 |
当斜率存在时,设直线l的方程为y=k(x-1),A(x1,y1),B(x2,y2),
则有
|
则x1+x2=
| 4k2 |
| 1+2k2 |
| 2k2-2 |
| 1+2k2 |
∴|AB|=
| 1+k2 |
(
|
| 1+k2 |
| 1+2k2 |
| 8 |
4
| ||
| 3 |
解得k=±1
故直线l的方程为:x+y-1=0或x-y-1=0
(2)原点到直线x+y-1=0或x-y-1=0的距离d=
| 1 | ||
|
| ||
| 2 |
故△OAB的面积S=
| 1 |
| 2 |
4
| ||
| 3 |
| ||
| 2 |
| 2 |
| 3 |

练习册系列答案
相关题目
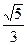 ,短轴长为4,求椭圆标准方程
,短轴长为4,求椭圆标准方程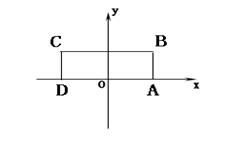
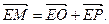 (Ⅰ)求点M的轨迹方程;
(Ⅰ)求点M的轨迹方程;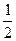 ),过点F的直线l与点M的轨迹相交于Q、R两点,且
),过点F的直线l与点M的轨迹相交于Q、R两点,且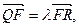 求实数
求实数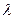 的取值范围.
的取值范围.
