题目内容
(本题满分12分)给定椭圆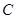 :
: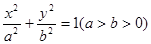 ,称圆心在原点
,称圆心在原点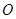 ,半径为
,半径为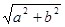 的圆是椭圆
的圆是椭圆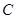 的“准圆”。若椭圆
的“准圆”。若椭圆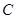 的一个焦点为
的一个焦点为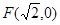 ,其短轴上的一个端点到
,其短轴上的一个端点到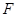 的距离为
的距离为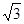 .
.
(Ⅰ)求椭圆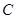 的方程和其“准圆”方程.
的方程和其“准圆”方程.
(Ⅱ)点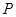 是椭圆
是椭圆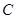 的“准圆”上的一个动点,过动点
的“准圆”上的一个动点,过动点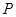 作直线
作直线 使得
使得 与椭圆
与椭圆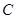 都只有一个交点,且
都只有一个交点,且 分别交其“准圆”于点
分别交其“准圆”于点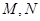 ,求证:
,求证: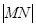 为定值.
为定值.
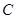 :
: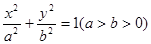 ,称圆心在原点
,称圆心在原点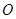 ,半径为
,半径为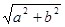 的圆是椭圆
的圆是椭圆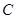 的“准圆”。若椭圆
的“准圆”。若椭圆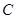 的一个焦点为
的一个焦点为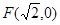 ,其短轴上的一个端点到
,其短轴上的一个端点到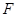 的距离为
的距离为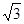 .
.(Ⅰ)求椭圆
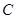 的方程和其“准圆”方程.
的方程和其“准圆”方程.(Ⅱ)点
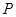 是椭圆
是椭圆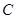 的“准圆”上的一个动点,过动点
的“准圆”上的一个动点,过动点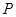 作直线
作直线 使得
使得 与椭圆
与椭圆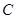 都只有一个交点,且
都只有一个交点,且 分别交其“准圆”于点
分别交其“准圆”于点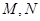 ,求证:
,求证: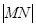 为定值.
为定值.(Ⅰ)
(Ⅱ)根据 斜率情况进行分类讨论,分别证明知直线
斜率情况进行分类讨论,分别证明知直线 垂直,从而
垂直,从而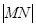 =4
=4

(Ⅱ)根据
 斜率情况进行分类讨论,分别证明知直线
斜率情况进行分类讨论,分别证明知直线 垂直,从而
垂直,从而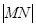 =4
=4解:(Ⅰ) ,
, 椭圆方程为
椭圆方程为 ……2分
……2分
准圆方程为 。 …………3分
。 …………3分
(Ⅱ)①当 中有一条无斜率时,不妨设
中有一条无斜率时,不妨设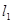 无斜率,因为
无斜率,因为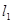 与椭圆只有一个公共点,则其方程为
与椭圆只有一个公共点,则其方程为 ,当
,当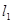 方程为
方程为 时,此时
时,此时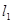 与准圆交于点
与准圆交于点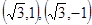 ,
,
此时经过点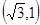 (或
(或 )且与椭圆只有一个公共点的直线是
)且与椭圆只有一个公共点的直线是 (或
(或 ),
),
即 为
为 (或
(或 ),显然直线
),显然直线 垂直;
垂直;
同理可证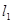 方程为
方程为 时,直线
时,直线 垂直. …………………………6分
垂直. …………………………6分
②当 都有斜率时,设点
都有斜率时,设点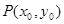 ,其中
,其中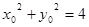 .
.
设经过点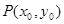 与椭圆只有一个公共点的直线为
与椭圆只有一个公共点的直线为 ,
,
则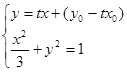 消去
消去 ,得
,得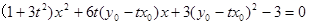 .
.
由 化简整理得:
化简整理得: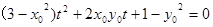 .…………………………8分
.…………………………8分
因为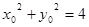 ,所以有
,所以有 .
.
设 的斜率分别为
的斜率分别为 ,因为
,因为 与椭圆只有一个公共点,
与椭圆只有一个公共点,
所以 满足上述方程
满足上述方程 ,
,
所以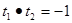 ,即
,即 垂直. …………………………10分
垂直. …………………………10分
综合①②知:因为 经过点
经过点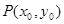 ,又分别交其准圆于点
,又分别交其准圆于点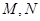 ,且
,且 垂直,所以线段
垂直,所以线段 为准圆
为准圆 的直径,所以
的直径,所以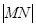 =4. ………………………12分
=4. ………………………12分
 ,
, 椭圆方程为
椭圆方程为 ……2分
……2分准圆方程为
 。 …………3分
。 …………3分(Ⅱ)①当
 中有一条无斜率时,不妨设
中有一条无斜率时,不妨设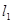 无斜率,因为
无斜率,因为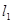 与椭圆只有一个公共点,则其方程为
与椭圆只有一个公共点,则其方程为 ,当
,当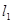 方程为
方程为 时,此时
时,此时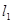 与准圆交于点
与准圆交于点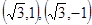 ,
,此时经过点
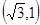 (或
(或 )且与椭圆只有一个公共点的直线是
)且与椭圆只有一个公共点的直线是 (或
(或 ),
),即
 为
为 (或
(或 ),显然直线
),显然直线 垂直;
垂直;同理可证
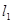 方程为
方程为 时,直线
时,直线 垂直. …………………………6分
垂直. …………………………6分②当
 都有斜率时,设点
都有斜率时,设点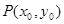 ,其中
,其中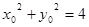 .
.设经过点
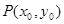 与椭圆只有一个公共点的直线为
与椭圆只有一个公共点的直线为 ,
,则
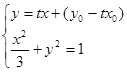 消去
消去 ,得
,得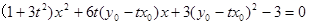 .
.由
 化简整理得:
化简整理得: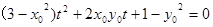 .…………………………8分
.…………………………8分因为
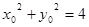 ,所以有
,所以有 .
.设
 的斜率分别为
的斜率分别为 ,因为
,因为 与椭圆只有一个公共点,
与椭圆只有一个公共点,所以
 满足上述方程
满足上述方程 ,
,所以
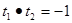 ,即
,即 垂直. …………………………10分
垂直. …………………………10分综合①②知:因为
 经过点
经过点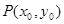 ,又分别交其准圆于点
,又分别交其准圆于点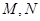 ,且
,且 垂直,所以线段
垂直,所以线段 为准圆
为准圆 的直径,所以
的直径,所以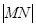 =4. ………………………12分
=4. ………………………12分
练习册系列答案
相关题目
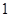 的圆周上.从整点
的圆周上.从整点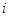 到整点
到整点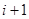 的向量记作
的向量记作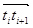 ,则
,则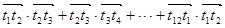 = .
= .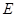 :
: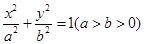 的左、右焦点分别为
的左、右焦点分别为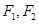 ,焦距为2,,过
,焦距为2,,过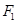 作垂直于椭圆长轴的弦长
作垂直于椭圆长轴的弦长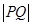 为3.
为3. 求椭圆
求椭圆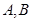 两点.并判断是否存在直线l使得
两点.并判断是否存在直线l使得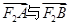 的夹角为钝角,若存在,求出l的斜率k的取值范围。
的夹角为钝角,若存在,求出l的斜率k的取值范围。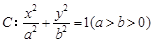 的离心率为
的离心率为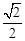 ,其中左焦点
,其中左焦点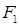 (-2,0).
(-2,0). 的右焦点为
的右焦点为 ,右准线
,右准线  与两条渐近线交于
与两条渐近线交于 两点,如果
两点,如果 是等边三角形,则双曲线的离心率
是等边三角形,则双曲线的离心率 的值为( )
的值为( )



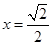 围成的三角形区域(包括边界)为E, P(x, y)为该区域内的一动点,则目标函数z=x-2y的最小值为________.
围成的三角形区域(包括边界)为E, P(x, y)为该区域内的一动点,则目标函数z=x-2y的最小值为________.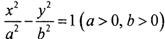 上•,
上•,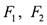 是这条双曲线的两个焦点,
是这条双曲线的两个焦点,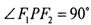 ,且
,且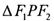 的三条边长成等差数列,则此双曲线的离心率是
的三条边长成等差数列,则此双曲线的离心率是  中的抛物线
中的抛物线 ,直线
,直线 过焦点
过焦点 且与抛物线相交于
且与抛物线相交于 ,
, 两点.
两点. 时,用
时,用 表示
表示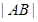 的长度;
的长度; 且三角形
且三角形 的面积为4时,求直线
的面积为4时,求直线
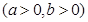 的离心率为
的离心率为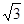 ,且它的一条准线与抛物
,且它的一条准线与抛物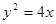 的准线重合,则此双曲线的方程是( )
的准线重合,则此双曲线的方程是( )


