题目内容
设双曲线4x2-y2=1的两条渐近线与直线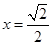 围成的三角形区域(包括边界)为E, P(x, y)为该区域内的一动点,则目标函数z=x-2y的最小值为________.
围成的三角形区域(包括边界)为E, P(x, y)为该区域内的一动点,则目标函数z=x-2y的最小值为________.
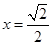 围成的三角形区域(包括边界)为E, P(x, y)为该区域内的一动点,则目标函数z=x-2y的最小值为________.
围成的三角形区域(包括边界)为E, P(x, y)为该区域内的一动点,则目标函数z=x-2y的最小值为________.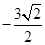
试题分析:双曲线4x2-y2=1的渐近线为
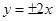 ,画出可行域,再画出目标函数,通过平移可知在
,画出可行域,再画出目标函数,通过平移可知在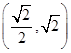 处取到最小值,最小值为
处取到最小值,最小值为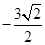 .
.点评:解决线性规划问题的关键是正确画出可行域和目标函数,确定取得最值点的点.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
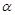 、
、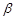 、
、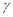 两两垂直,定点
两两垂直,定点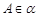 ,A到
,A到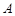 的距离,则P点轨迹上的点到
的距离,则P点轨迹上的点到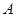 是椭圆
是椭圆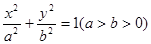 的右顶点,若点
的右顶点,若点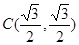 在椭圆上,且满足
在椭圆上,且满足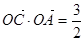 .(其中
.(其中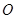 为坐标原点)
为坐标原点)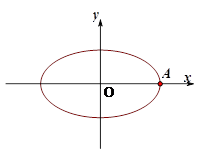
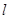 与椭圆交于两点
与椭圆交于两点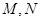 ,当
,当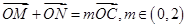 时,求
时,求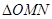 面积的最大值.
面积的最大值. 的焦点与双曲线
的焦点与双曲线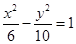 的右焦点重合,则实数
的右焦点重合,则实数 的值是 .
的值是 . 的两条渐近线的夹角大小等于 .
的两条渐近线的夹角大小等于 .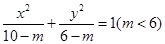 与曲线
与曲线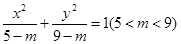 的( )
的( )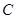 :
: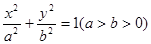 ,称圆心在原点
,称圆心在原点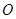 ,半径为
,半径为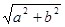 的圆是椭圆
的圆是椭圆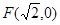 ,其短轴上的一个端点到
,其短轴上的一个端点到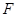 的距离为
的距离为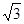 .
.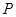 是椭圆
是椭圆 使得
使得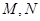 ,求证:
,求证: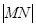 为定值.
为定值. 的焦点F,与抛物线交于两点A,B,
的焦点F,与抛物线交于两点A,B,
 的方程;
的方程; 的面积S的最大值;
的面积S的最大值; +
+ =1的右焦点作一条斜率为2的直线与椭圆交于A、B两点,O为坐标原点,求弦AB的长_______
=1的右焦点作一条斜率为2的直线与椭圆交于A、B两点,O为坐标原点,求弦AB的长_______